
How do you solve $\dfrac{3}{2}y-y=4+0.5y$ ?
Answer
550.8k+ views
Hint: We first add the two terms on the left hand side of the equation, as they are like terms and then find out that the left hand side is exactly equal to the right hand side. Thus, the equation is independent of $y$ and thus has infinite solutions.
Complete step by step solution:
The given equation that we have at our hand is,
$\dfrac{3}{2}y-y=4+0.5y$
We see two algebraic terms of the same variable on the left hand side of the above equation. So, the first thing that comes to our mind is to add them. We proceed by adding them after taking $y$ common from both the terms and adding the arithmetic terms. After adding the two terms $\dfrac{3}{2}y$ and $-y$ in the above mentioned method, the above equation thus becomes,
$\Rightarrow \left( \dfrac{3}{2}-1 \right)y=4+0.5y$
Performing the subtraction of the two terms $\dfrac{3}{2}$ and $1$ , the above equation thus becomes,
$\Rightarrow \left( \dfrac{1}{2} \right)y=4+0.5y$
Now, we know that the fraction $\dfrac{1}{2}$ is nothing but equal to the decimal $0.5$ . So, rewriting the above equation by converting the $\dfrac{1}{2}$ to $0.5$ , we get,
$\Rightarrow 0.5y=4+0.5y$
If we carefully observe the above equation, we can clearly see that we can easily cancel off $0.5y$ from both the sides of the above equation. This means that the above equation does not respond to any value of $y$ . In other words, we can say that the above equation is independent of $y$ as it gets cancelled off from both the sides of the equation. Being independent of $y$ , the equation gives the same results for any value of $y$ . In other words, we can say that infinite or all values of $y$ satisfy the above equation.
Therefore, we can conclude that the given equation has infinite solutions.
Note: In these types of problems, unlike other problems, it is better not to bring all the algebraic terms to one side. The algebraic terms should be simplified on the two sides separately and their coefficients should be compared for infinite solution possibility. These can also solve by taking the two sides of the equation as two separate lines and then plot the lines on a graph. The point of intersection gives the solution. Here, the lines being parallel, have no solution.
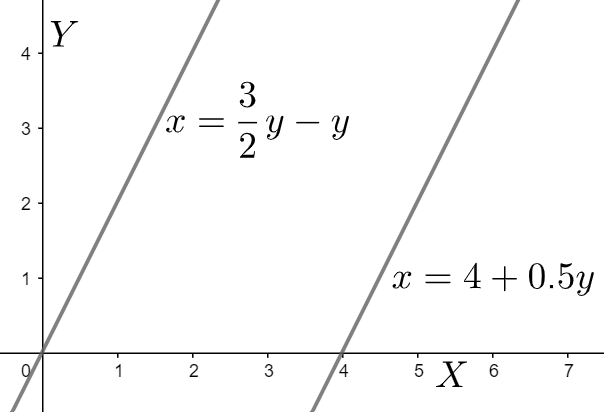
Complete step by step solution:
The given equation that we have at our hand is,
$\dfrac{3}{2}y-y=4+0.5y$
We see two algebraic terms of the same variable on the left hand side of the above equation. So, the first thing that comes to our mind is to add them. We proceed by adding them after taking $y$ common from both the terms and adding the arithmetic terms. After adding the two terms $\dfrac{3}{2}y$ and $-y$ in the above mentioned method, the above equation thus becomes,
$\Rightarrow \left( \dfrac{3}{2}-1 \right)y=4+0.5y$
Performing the subtraction of the two terms $\dfrac{3}{2}$ and $1$ , the above equation thus becomes,
$\Rightarrow \left( \dfrac{1}{2} \right)y=4+0.5y$
Now, we know that the fraction $\dfrac{1}{2}$ is nothing but equal to the decimal $0.5$ . So, rewriting the above equation by converting the $\dfrac{1}{2}$ to $0.5$ , we get,
$\Rightarrow 0.5y=4+0.5y$
If we carefully observe the above equation, we can clearly see that we can easily cancel off $0.5y$ from both the sides of the above equation. This means that the above equation does not respond to any value of $y$ . In other words, we can say that the above equation is independent of $y$ as it gets cancelled off from both the sides of the equation. Being independent of $y$ , the equation gives the same results for any value of $y$ . In other words, we can say that infinite or all values of $y$ satisfy the above equation.
Therefore, we can conclude that the given equation has infinite solutions.
Note: In these types of problems, unlike other problems, it is better not to bring all the algebraic terms to one side. The algebraic terms should be simplified on the two sides separately and their coefficients should be compared for infinite solution possibility. These can also solve by taking the two sides of the equation as two separate lines and then plot the lines on a graph. The point of intersection gives the solution. Here, the lines being parallel, have no solution.
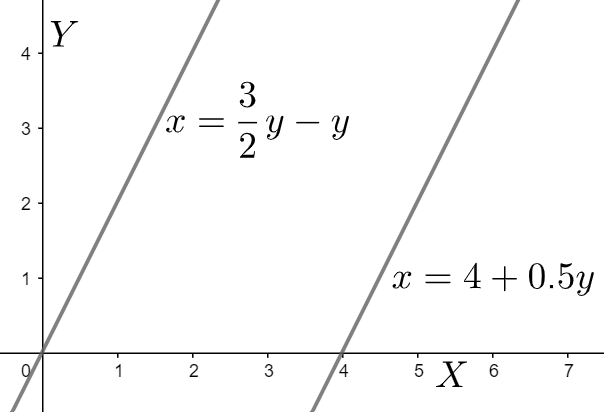
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 English: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Master Class 7 English: Engaging Questions & Answers for Success

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

Advantages and disadvantages of science

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE

What are the 12 elements of nature class 8 chemistry CBSE





