Question

How do you solve and graph \[4x+5>25\]?

Answer 1

Hint: Rearrange the terms by taking the constants to the R.H.S. and leaving the terms containing the variable x to the L.H.S. Now, simplify the R.H.S. and then make the coefficient of x equal to 1 by dividing both sides with 4. Leave the inequality sign as it is. Draw a line x = 5 and consider the suitable part of the graph according to the simplified inequality obtained.

Complete step by step answer:
Here, we have been provided with the inequality \[4x+5>25\] and we are asked to solve it and draw the graph.
Now, rearranging by taking the constant terms to the R.H.S. and leaving the terms containing the variable x in the L.H.S., we get,
\[\begin{align}
  & \Rightarrow 4x+5>25 \\
 & \Rightarrow 4x>25-5 \\
 & \Rightarrow 4x>20 \\
\end{align}\]
Dividing both the sides with 4, we get,
\[\Rightarrow \dfrac{4x}{4}>\dfrac{20}{4}\]
\[\Rightarrow x>5\] - (1)
Here, as you can see that we have not changed the inequality sign after dividing both the sides with 4. This is because we have divided both the sides with a positive number. If we would have divided with a negative number then it would have divided with a negative number then it would have been necessary to reverse the inequality sign.
Now, let us draw the graph of inequality obtained in (1). To do this first we have to remove the inequality sign and replace it with ‘=’ sign and draw the required line. So, we have,
\[\Rightarrow x=5\]
Drawing the line x = 5, we get,

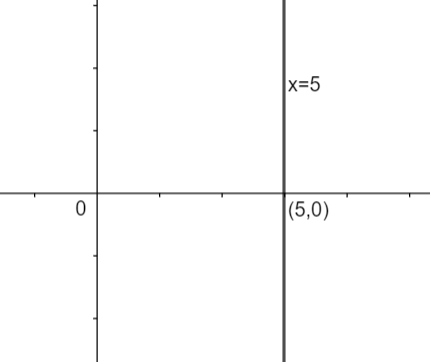
Now, considering inequation (1), i.e., x > 5, here we can clearly see that we have to select that part of the graph in which x will be greater than 5. So, in the above graph we have to select the right side of the graph x = 5. Therefore, we have,

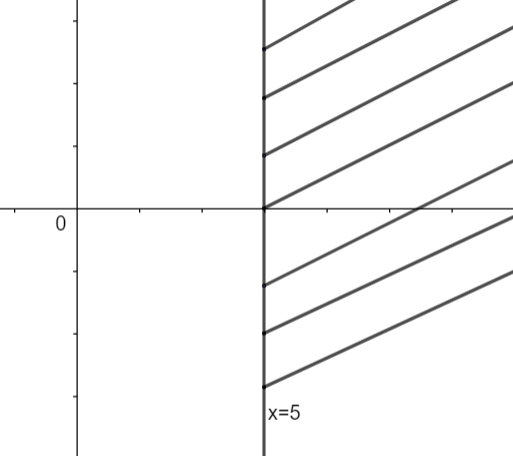
So, the above graph represents the graphical solution of our inequality.

Note:
One may note that there are not many differences in solving and graphing an equality and an inequality. We need the help of equality while drawing the graph. One thing you may note that we do not consider the value x = 5 in our graph so it will be better to use the dashed line instead of a solid line, however we have used a solid line. Always remember the rules of reversing the direction of inequality. The direction is only reversed when we take reciprocal or divide and multiply both the sides with a negative number.