Question

How do you solve $4x-12>4$ ?

Answer 1

Hint: We solve any inequality problem by bringing the arithmetic terms to one side and the algebraic or the $x$ related terms to the other side. Then after performing the various operations like addition, division, etc, we arrive at the solution. Here, we take $12$ to the right hand side and then divide the two sides by $4$ .

Complete step by step solution:
The given inequality is
 $4x-12>4$
We have to solve this inequality simply just as we solve an equation. For this, we need to bring all the $x$ related terms to one side and other arithmetic terms to the other side. But here, as there is only one $x$ related term, we need not do this operation. So, we simply bring the arithmetic terms to the right hand side. To do this, we add $12$ to both sides of the given above inequality. The inequality thus becomes,
$\Rightarrow 4x-12+12>4+12$
Upon simplification, the above inequality thus becomes,
$\Rightarrow 4x>4+12$
Adding $4$ and $12$ , the above equation becomes,
$\Rightarrow 4x>16$
Dividing both sides of the above equation by $4$ , the above equation thus becomes,
$\Rightarrow \dfrac{4x}{4}>\dfrac{16}{4}$
Upon simplification, the above inequality thus becomes,
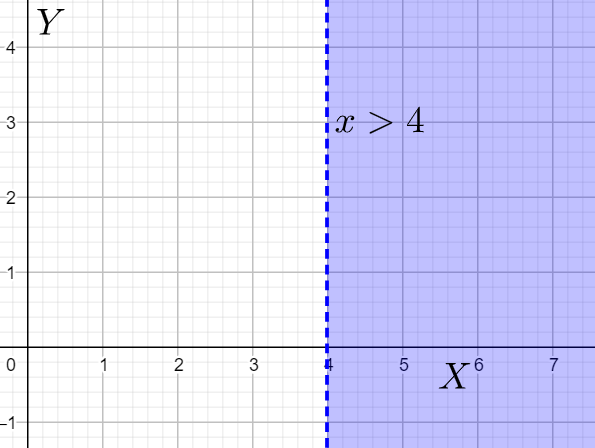
$\Rightarrow x>4$
This means that all the values of $x$ which are greater than $4$ are the solution to the given inequality or that they satisfy the given inequality.
Therefore, we can conclude that the solution of the given inequality is $x>4$ .

Note: We should be careful while grouping the arithmetic and the algebraic terms and should take care of the signs of the terms. While multiplying the two sides of the inequality by a negative number, or while taking the reciprocals of both the sides, we should reverse the inequality sign.