Question

How do you solve $3y-20=8y$?

Answer 1

Hint: The given equation which is written as $3y-20=8y$ is a single variable equation in $y$ whose highest power is equal to one. This means that the given equation is a linear equation in one variable, and so it will have a unique solution. We can equate the LHS and the RHS of the given equation to a variable $x$ to get the equations $x=3y-20$ and $x=8y$, which represent the equations of straight lines. On plotting these on a graph, we will obtain the solution from the y-coordinate of the point of intersection.

Complete step-by-step solution:
The given equation is
$3y-20=8y$
Since the LHS and the RHS of the above equation are equal to each other, we can equate both of them to $x$ to get pair of the equations
$\begin{align}
  & \Rightarrow x=3y-20 \\
 & \Rightarrow x=8y \\
\end{align}$
Since the above two equations are linear in both x and y, so they both represent the equation of a straight line. Plotting their graphs, we have the following figure.

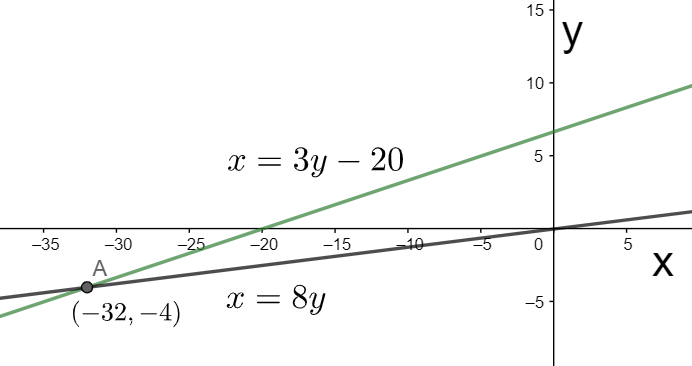
From the above figure, we note that the coordinates of the point of intersection of the two lines are $\left( -32,-4 \right)$.
Hence the solution of the given equation, given by the y-coordinate of the intersection points, is $y=-4$.

Note: We must not write both the x and the y coordinates as the final answer. We must remember that the equation given to us was a single variable equation, and we converted it into a pair of two variable equations. Also, since the equation was in terms of the variable y, so the y-coordinate of the intersection point gave the final solution, and not the x-coordinate.