Question

How do you solve $3y=11-2x$ and $3x=y-11$?

Answer 1

Hint: In the above question, we are given a pair of linear equations in two variables. So they together represent a pair of two straight lines. We can write them into the slope intercept form given by $y=mx+c$ and plot their respective graphs. The solution of the given pair of equations will be obtained from the coordinates of the point of intersection of the two straight lines from the graph plotted.

Complete step-by-step solution:
The two equations given in the above question are the linear equations in two variables. We know that a linear equation in two variables represents a straight line. So the given equations represent the pair of straight lines.
For solving the given equations, we can plot their graphs and obtain the solution as the coordinates of the point of intersection. For plotting their graphs, we must write them in the slope intercept form, which is $y=mx+c$.
Considering the first equation, we have
$\Rightarrow 3y=11-2x$
Dividing both sides by $3$ we get
$\begin{align}
  & \Rightarrow \dfrac{3y}{3}=\dfrac{11-2x}{3} \\
 & \Rightarrow y=-\dfrac{2}{3}x+\dfrac{11}{3}.......\left( i \right) \\
\end{align}$
Now, considering the second equation, we have
$\begin{align}
  & \Rightarrow 3x=y-11 \\
 & \Rightarrow y-11=3x \\
\end{align}$
Adding $11$ both the sides, we get
\[\begin{align}
  & \Rightarrow y-11+11=3x+11 \\
 & \Rightarrow y=3x+11.........\left( ii \right) \\
\end{align}\]
Plotting the graphs of the equations (i) and (ii), we get the below figure.

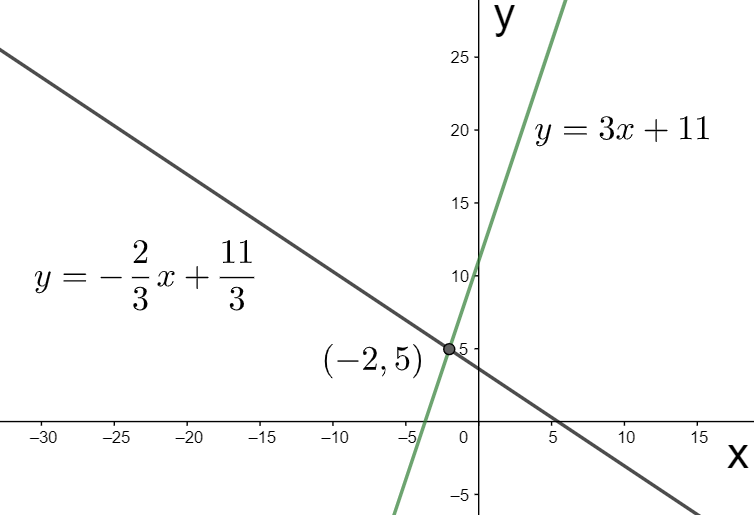
From the above graph, we get the coordinates of the intersection point as $\left( -2,5 \right)$.
Hence, the solution of the given equations is $x=-2$ and $y=5$.

Note: We can also solve the above question by using the substitution method. For that we have to obtain the value of the variable y in terms of the variable x from the second equation $3x=y-11$ and substitute it in the first equation $3y=11-2x$ to get an equation in x. On solving the equation obtained, we will get the value of x which after substituting into any of the two equations will yield the value of y.