
How do you solve $3x - y = 10$ and $ - x + y = - 4$?
Answer
545.7k+ views
Hint:
First we have to make the first linear equation in Slope-intercept form and then calculate the value of $y$ for any two arbitrary values of $x$. Next make a table of these values of $x$ and $y$. Next plot the obtained points on the graph paper and draw a line passing through these points. Now repeat the process with the second equation and determine the solution of the given system of equations using the graph obtained.
Formula used:
Slope Intercept of a line:
The equation of a line with slope $m$ and making an intercept $c$ on $y$-axis is $y = mx + c$.
Complete step by step solution:
First, we have to move $3x$ to the right side of the equation, $3x - y = 10$. Thus, subtracting $3x$ to both sides of the equation.
$ \Rightarrow - y = 10 - 3x$
Now, multiply both sides of the equation by $\left( { - 1} \right)$.
$ \Rightarrow y = 3x - 10$
Now, we have to calculate the value of $y$ for any two arbitrary values of $x$. Thus, finding the value of $y$ when $x = 1$ and $x = 2$.
When $x = 1$, $y = 3\left( 1 \right) - 10 = - 7$
When $x = 2$, $y = 3\left( 2 \right) - 10 = - 4$
Now we have to make a table of these values of $x$ and $y$.
Now we have to plot the points $A\left( {1, - 7} \right)$ and $B\left( {2, - 4} \right)$ on the graph paper and draw a line passing through $A$ and $B$, we get the graph of equation $3x - y = 10$.
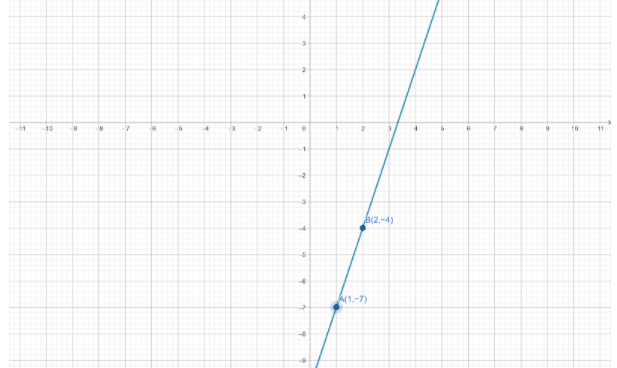
Now we have to make the second equation in Slope-intercept form. Thus, adding $x$ to both sides of the equation.
$y = - 4 + x$
Now, we have to calculate the value of $y$ for any two arbitrary value of $x$. Thus, finding the value of $y$ when $x = 0$ and $x = - 1$.
When $x = 0$, $y = - 4 + 0 = - 4$
When $x = - 1$, $y = - 4 + \left( { - 1} \right) = - 5$
Now we have to make a table of these values of $x$ and $y$.
Now we have to plot the points $C\left( {0, - 4} \right)$ and $D\left( { - 1, - 5} \right)$ on the graph paper and draw a line passing through $C$ and $D$, we obtain the graph of the equation $ - x + y = - 4$.
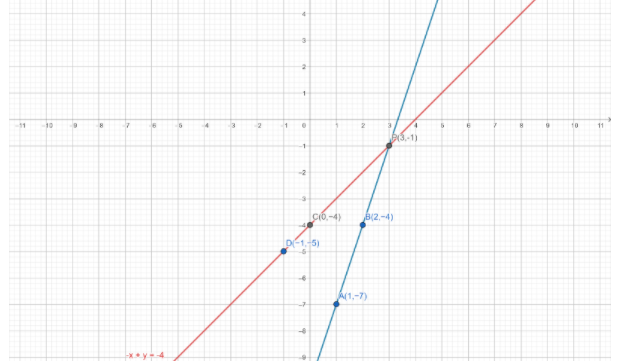
Clearly, two lines intersect at point $P\left( {3, - 1} \right)$.
Final solution: Hence, $x = 3$ and $y = - 1$ is the solution of the given system.
Note:
We can directly find the solution of a given system by Method of Elimination.
Method of Elimination:
In this method, we eliminate one of the two variables to obtain an equation in one variable which can be easily solved. Putting the value of this variable in any one of the given equations, the value of another variable can be obtained.
Step by step solution:
The given system of equations is
$3x - y = 10$
$ - x + y = - 4$
We can eliminate the $y$ variable by adding the two equations.
So, adding given equations, we get
$ \Rightarrow 2x = 6$
Now, divide both sides of the equation by $2$.
$ \Rightarrow x = 3$
Now, substitute the value of $x$ in equation $ - x + y = - 4$ and find the value of $y$.
$ \Rightarrow - 3 + y = - 4$
$ \Rightarrow y = - 1$
Final solution: Hence, $x = 3$ and $y = - 1$ is the solution of the given system.
First we have to make the first linear equation in Slope-intercept form and then calculate the value of $y$ for any two arbitrary values of $x$. Next make a table of these values of $x$ and $y$. Next plot the obtained points on the graph paper and draw a line passing through these points. Now repeat the process with the second equation and determine the solution of the given system of equations using the graph obtained.
Formula used:
Slope Intercept of a line:
The equation of a line with slope $m$ and making an intercept $c$ on $y$-axis is $y = mx + c$.
Complete step by step solution:
First, we have to move $3x$ to the right side of the equation, $3x - y = 10$. Thus, subtracting $3x$ to both sides of the equation.
$ \Rightarrow - y = 10 - 3x$
Now, multiply both sides of the equation by $\left( { - 1} \right)$.
$ \Rightarrow y = 3x - 10$
Now, we have to calculate the value of $y$ for any two arbitrary values of $x$. Thus, finding the value of $y$ when $x = 1$ and $x = 2$.
When $x = 1$, $y = 3\left( 1 \right) - 10 = - 7$
When $x = 2$, $y = 3\left( 2 \right) - 10 = - 4$
Now we have to make a table of these values of $x$ and $y$.
| $x$ | $1$ | $2$ |
| $y$ | $ - 7$ | $ - 4$ |
Now we have to plot the points $A\left( {1, - 7} \right)$ and $B\left( {2, - 4} \right)$ on the graph paper and draw a line passing through $A$ and $B$, we get the graph of equation $3x - y = 10$.

Now we have to make the second equation in Slope-intercept form. Thus, adding $x$ to both sides of the equation.
$y = - 4 + x$
Now, we have to calculate the value of $y$ for any two arbitrary value of $x$. Thus, finding the value of $y$ when $x = 0$ and $x = - 1$.
When $x = 0$, $y = - 4 + 0 = - 4$
When $x = - 1$, $y = - 4 + \left( { - 1} \right) = - 5$
Now we have to make a table of these values of $x$ and $y$.
| $x$ | $0$ | $ - 1$ |
| $y$ | $ - 4$ | $ - 5$ |
Now we have to plot the points $C\left( {0, - 4} \right)$ and $D\left( { - 1, - 5} \right)$ on the graph paper and draw a line passing through $C$ and $D$, we obtain the graph of the equation $ - x + y = - 4$.

Clearly, two lines intersect at point $P\left( {3, - 1} \right)$.
Final solution: Hence, $x = 3$ and $y = - 1$ is the solution of the given system.
Note:
We can directly find the solution of a given system by Method of Elimination.
Method of Elimination:
In this method, we eliminate one of the two variables to obtain an equation in one variable which can be easily solved. Putting the value of this variable in any one of the given equations, the value of another variable can be obtained.
Step by step solution:
The given system of equations is
$3x - y = 10$
$ - x + y = - 4$
We can eliminate the $y$ variable by adding the two equations.
So, adding given equations, we get
$ \Rightarrow 2x = 6$
Now, divide both sides of the equation by $2$.
$ \Rightarrow x = 3$
Now, substitute the value of $x$ in equation $ - x + y = - 4$ and find the value of $y$.
$ \Rightarrow - 3 + y = - 4$
$ \Rightarrow y = - 1$
Final solution: Hence, $x = 3$ and $y = - 1$ is the solution of the given system.
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 English: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Master Class 7 English: Engaging Questions & Answers for Success

Trending doubts
Difference Between Plant Cell and Animal Cell

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Which places in India experience sunrise first and class 9 social science CBSE

Who is eligible for RTE class 9 social science CBSE

What is pollution? How many types of pollution? Define it

Name 10 Living and Non living things class 9 biology CBSE




