Question

How do you simplify \[\sqrt{250}\] ?

Answer 1

Hint: As the number is not too large, therefore we can use the prime factorization method, first find all the prime factors of the given number whose square root we need to find, after finding all the prime factors make the pair of each factor (if there) and that will come out from the radical root then multiply all those pairs and the unpaired remains inside the radical sign.

Complete step by step solution:
Using the prime factorization method:
First, we need to find all the prime factors of this number

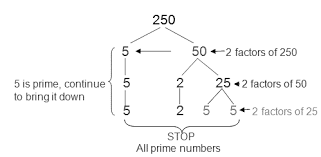
\[\Rightarrow 250=2\times 5\times 5\times 5\]
Now pairing these prime factors
\[\Rightarrow 250=2\times 5\times (5\times 5)\]
Here, only one pair exists since for others we don’t have anymore \[2\] and \[5\]
\[\Rightarrow \sqrt{250}=\sqrt{2\times 5\times (5\times 5)}\]
So that \[5\] from the pair will come out
\[\Rightarrow \sqrt{250}=5\sqrt{2\times 5}\]
\[\Rightarrow \sqrt{250}=5\sqrt{10}\]

Hence, \[\sqrt{250}=5\sqrt{10}\]

Note:
Since the number was not too large, therefore, we have used the prime factorization method as it was quite simple although we can use the division method too. While factorization notes that all factors must be prime.