Question

How do you simplify \[\sec (\arctan (4x))\]?

Answer 1

Hint: We will consider the inner function as an angle. Then we will eliminate the function \[\arctan \] from the resulting expression. Next, we will draw a right triangle based on the expression. Finally, we will find \[\sec \] of the angle we have considered.

Formula used:
 \[\tan (\arctan (x)) = x\]

Complete step by step solution:
We are required to simplify the expression \[\sec (\arctan (4x))\].
Let us begin by denoting the innermost function, which is \[\arctan (4x)\] as an angle \[\theta \]. We get
\[\theta = \arctan (4x)\] ………\[(1)\]
Let us try to eliminate the function \[\arctan \] from equation \[(1)\] by taking \[\tan \] on both sides of equation \[(1)\]. This gives us
\[\tan \theta = \tan (\arctan (4x))\] ………..\[(2)\]
We will use the property \[\tan (\arctan (x)) = x\] on the RHS of equation \[(2)\] to get the following expression:
\[\tan \theta = 4x\] ………\[(3)\]
Let us consider a right triangle ABC with right-angle \[\angle B\] as in the figure. Let us take \[\theta \] as the angle between the sides \[AC\] and \[BC\].

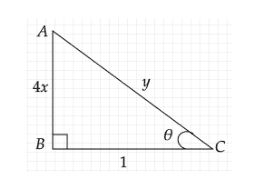
Now, from equation \[(3)\], we can write
\[\tan \theta = \dfrac{{4x}}{1}\]
We know that in a right-triangle ABC,
\[\tan \theta = \dfrac{{{\rm{opp}}{\rm{. side}}}}{{{\rm{adj}}{\rm{. side}}}}\]. Compared with the above equation, we can take the opposite side of the right-triangle as \[4x\] units and the adjacent side as \[1\] unit.
Now, we have to find the hypotenuse of the right triangle with sides \[4x\] units and \[1\] units.
By Pythagoras theorem, we have \[A{C^2} = A{B^2} + B{C^2}\]. Substituting \[AC = y,AB = 4x\] and \[BC = 1\], we get
\[{y^2} = {(4x)^2} + {1^2}\]
Taking square root on both sides of the above expression, we get
\[y = \sqrt {16{x^2} + 1} \] ……..\[(4)\]
We are supposed to find the value of \[\sec (\arctan (4x))\], which from equation \[(1)\] is the same as \[\sec \theta \].
We know that \[\sec \theta = \dfrac{{{\rm{hypotenuse}}}}{{{\rm{adj}}{\rm{. side}}}}\]. So, from triangle ABC and equation \[(4)\], we get
\[\sec \theta = \dfrac{{\sqrt {16{x^2} + 1} }}{1} = \sqrt {16{x^2} + 1} \]

Note:
The functions \[\tan \] and \[\arctan \] are inverse functions. We have used the property \[\tan (\arctan (x)) = x\] to eliminate the function \[\arctan \], since we cannot use that function in a right-angled triangle. Similarly, we have properties \[\sin (\arcsin (x)) = x\] and \[\cos (\arccos (x)) = x\].