Question

How do you prove $ 1 + {\cot ^2}x = \cos e{c^2}x $ ?

Answer 1

Hint: The given equation $ 1 + {\cot ^2}x = \cos e{c^2}x $ is a famous trigonometric identity. To prove this, we will use some relations. Take the LHS of the equation and try to prove $ LHS = RHS $ . Now, we know that $ \cot x = \dfrac{{\cos x}}{{\sin x}} $ , so put this in LHS of the given equation and simplify the equation and we will get $ LHS = RHS $ .

Complete step-by-step answer:
In this question, we are given a famous trigonometric identity and we need to prove it if its correct.
The given identity is: $ 1 + {\cot ^2}x = \cos e{c^2}x $ - - - - - - - - - - (1)
Here on the LHS we have $ 1 + {\cot ^2}x $ and on the RHS we have $ \cos e{c^2}x $ . And we need to prove that LHS is equal to RHS that is LHS=RHS.
Now, to prove this we need to use some trigonometric relations or formulas that can be applicable here.
First of all, let us take the LHS of equation (1).
 $ \to LHS = 1 + {\cot ^2}x $
Now, we know that cot is the ratio of cosine and sine. So, we can write cot is divided by sin.
 $
   \to \cot x = \dfrac{{\cos x}}{{\sin x}} \\
   \to {\cot ^2}x = \dfrac{{{{\cos }^2}x}}{{{{\sin }^2}x}} \;
  $
So, let us put this value in the LHS of equation (1). Therefore,
 $ \to LHS = 1 + {\cot ^2}x $
 $ = 1 + \dfrac{{{{\cos }^2}x}}{{{{\sin }^2}x}} $
Taking L.C.M, we get
 $ \to LHS = \dfrac{{{{\sin }^2}x + {{\cos }^2}x}}{{{{\sin }^2}x}} $
Now, we know that $ {\sin ^2}x + {\cos ^2}x = 1 $ . Therefore,
 $ \to LHS = \dfrac{1}{{{{\sin }^2}x}} $
Now, we know that the inverse of sine is cosecant. Hence, we can write 1 divided by sine as cosec.
 $
   \to \dfrac{1}{{\sin x}} = \cos ecx \\
   \to \dfrac{1}{{{{\sin }^2}x}} = \cos e{c^2}x \;
  $
Therefore, LHS will become
 $ \to LHS = \dfrac{1}{{{{\sin }^2}x}} = \cos e{c^2}x $
And our $ RHS = \cos e{c^2}x $ .
Hence, $ LHS = RHS $ is proved.
Hence, we have proved that $ 1 + {\cot ^2}x = \cos e{c^2}x $ .


Note: We can also prove the identity $ 1 + {\cot ^2}x = \cos e{c^2}x $ with another method.
For this, we will be using the triangle.

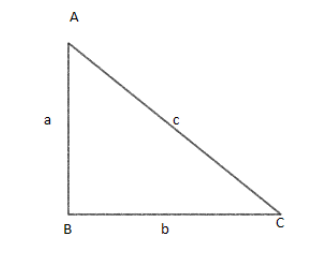
In the above triangle, using Pythagoras theorem,
 $ \to {a^2} + {b^2} = {c^2} $
Now, if we divide the above equation with $ {a^2} $ , we get
 $
   \to \dfrac{{{a^2}}}{{{a^2}}} + \dfrac{{{b^2}}}{{{a^2}}} = \dfrac{{{c^2}}}{{{a^2}}} \\
   \to 1 + {\left( {\dfrac{b}{a}} \right)^2} = {\left( {\dfrac{c}{a}} \right)^2} \\
  $
Now, in $ \Delta ABC $ , $ \cot = \dfrac{b}{a} $ and $ \cos ec = \dfrac{c}{a} $ . Hence, putting these values in above equation, we get
 $ \to 1 + {\cot ^2} = \cos e{c^2} $