Question

How do you plot $3+5i $?

Answer 1

Hint: The above question is in the complex number. In mathematics, a complex number is a number that can be expressed in the form $a+bi $, where a and b are real numbers, and $i$ is a symbol called the imaginary unit, and satisfying the equation ${{i }^{2}}=-1$.

Complete step by step solution:
We cannot plot complex numbers on a number line like real numbers, but we can still represent them graphically. To represent a complex number we need to address the two components of the number. We use the complex plane, which is a coordinate system in which the horizontal axis represents the real component and the vertical axis represents the imaginary component.
They are expressed in the ordered pairs (a, b), where a represents the coordinate for the horizontal axis and b represents the coordinate for the vertical axis.
The given complex number is:
$\Rightarrow 3+5i $
The points by which we can represent components of the given complex number on the complex plane are:
1. Determine the real and imaginary part of the complex number. Here the real part is 3 and the imaginary part is 5.
2. Move along the horizontal axis to show the real part of the number. It means we have to move three steps from the origin in the horizontal plane.
3. Move parallel to the vertical axis to show the imaginary part of the number. It means we will move vertically 5 steps from the origin.
4. Plot the points.

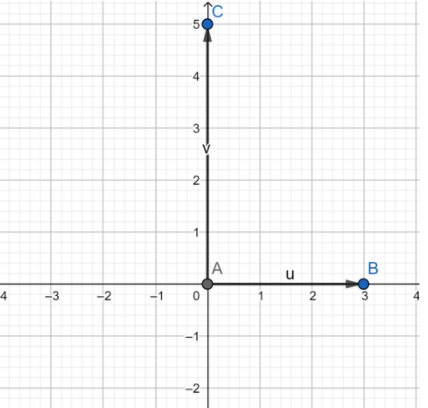
Hence we plotted the given complex number on a complex plane.

Note: In a complex plane, the horizontal axis is the real axis and the vertical axis is the imaginary axis. The complex numbers are represented in the $a+bi $ where a is the real part and b is the imaginary part, it means the a is plotted on the horizontal axis of the complex plane and b is plotted on vertical axis of the complex plane.