Question

How do you graph $y={{\left( x-1 \right)}^{2}}+2$?

Answer 1

Hint: We equate the given equation of parabolic curve with the general equation of ${{\left( x-\alpha \right)}^{2}}=4a\left( y-\beta \right)$. We find the number of x-intercepts and the value of the y-intercept. We also find the coordinates of the focus to place the curve in the graph.

Complete step by step answer:
The given equation $y={{\left( x-1 \right)}^{2}}+2$ is a parabolic curve.
We can convert the equation into ${{\left( x-1 \right)}^{2}}=y-2$.
We equate it with the general equation of parabola ${{\left( x-\alpha \right)}^{2}}=4a\left( y-\beta \right)$.
For the general equation $\left( \alpha ,\beta \right)$ is the vertex. 4a is the length of the latus rectum. The coordinate of the focus is $\left( \alpha ,\beta +a \right)$.
For the equation ${{\left( x-1 \right)}^{2}}=\left( y-2 \right)$
This gives the vertex as $\left( 1,2 \right)$. The length of the latus rectum is $4a=1$ which gives $a=\dfrac{1}{4}$.
We have to find the possible number of x-intercepts and the value of the y-intercept. The curve cuts the X and Y axis at certain points and those are the intercepts.

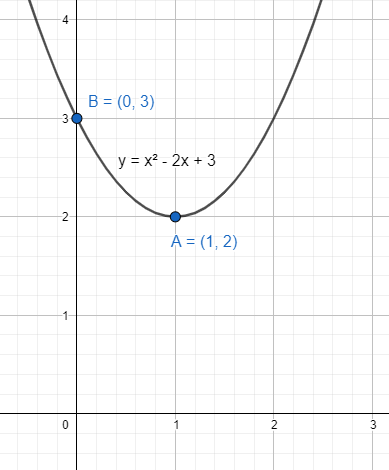
We first find the Y-axis intercepts. In that case for the Y-axis, we have to take the coordinate values of x as 0. Putting the value of $x=0$ in the equation ${{\left( x-1 \right)}^{2}}=\left( y-2 \right)$, we get
$\begin{align}
  & {{\left( 0-1 \right)}^{2}}=\left( y-2 \right) \\
 & \Rightarrow y-2=1 \\
 & \Rightarrow y=3 \\
\end{align}$
The intercept is the point $\left( 0,3 \right)$. The vertex is the intercept and it’s the only intercept on the Y-axis.
We first find the X-axis intercepts. In that case for X-axis, we have to take the coordinate values of y as 0. Putting the value of $y=0$ in the equation ${{\left( x-1 \right)}^{2}}=\left( y-2 \right)$, we get
\[\begin{align}
  & {{\left( x-1 \right)}^{2}}=\left( 0-2 \right) \\
 & \Rightarrow {{\left( x-1 \right)}^{2}}=-2 \\
\end{align}\]
There are no intercept points for X-axis.

Note:
The minimum point of the function $y={{\left( x-1 \right)}^{2}}+2$ is $y=2$. The graph is bounded at that point. But on the other side, the curve is open and not bounded. the general case of a parabolic curve is to be bounded at one side to mark the vertex.