
How do you graph
Answer
511.2k+ views
Hint: The above given question is a graph of linear equations in one variable. Since, we know that the slope intercept form of the line equation is given as y = mx + c, where m is the slope of the line and c is the y-intercept. In the given equation
Complete step by step answer:
We know that the above question is of the graph of linear equations in one variable.
We also know that the slope-intercept form of the linear equation is given y = mx + c, where m is the slope of the line and c is the y-intercept.
Now, we will compare the equation
After comparing we will get: m = 0 and
So, the slope of the line
Since slope of the line is equal to 0, hence the line will be parallel to the x-axis and also y-intercept is equal to
So, the required graph of the line
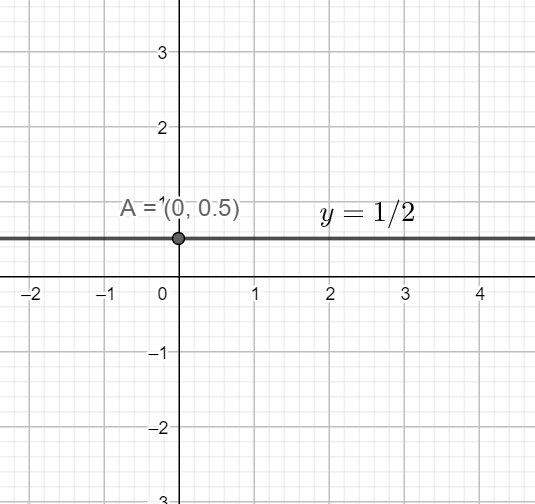
This is our required solution.
Note:
Student are required to note that in
Complete step by step answer:
We know that the above question is of the graph of linear equations in one variable.
We also know that the slope-intercept form of the linear equation is given y = mx + c, where m is the slope of the line and c is the y-intercept.
Now, we will compare the equation
After comparing we will get: m = 0 and
So, the slope of the line
Since slope of the line is equal to 0, hence the line will be parallel to the x-axis and also y-intercept is equal to
So, the required graph of the line

This is our required solution.
Note:
Student are required to note that in
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

Five things I will do to build a great India class 10 english CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Fill the blanks with proper collective nouns 1 A of class 10 english CBSE

10 examples of evaporation in daily life with explanations

Write a letter to the principal requesting him to grant class 10 english CBSE




