Question

How do you graph $y=6-1.25x$ ?

Answer 1

Hint: We are given a equation as $y=6-1.25x$ , we have to graph, to do so we will learn about the type of equation, depending upon that we will get that it will be a line or parabola arc etc, to find the graph we will find pair of ordered pair that satisfy the given equation, once we have those pair we will place them on the graph and then join the points, the graph obtained by this is the graph of $y=6-1.25x$ .

Complete step by step solution:
We are given $y=6-1.25x$ .
We can see it has a single variable ‘x’ and the power of that variable is ‘1’, so it is a one degree equation. Hence the graph formed by this will be a straight line.
If the equation may have power ‘2’ then it would be a parabola and similarly different for different powers of the equation.
Now to sketch a graph, we will find an ordered pair $\left( x,y \right)$ which must satisfy our equation $y=6-1.25x$ .
To do so, we will consider the value of ‘x’ by ourselves and use it in the equation to find the value of ‘y’.
So, we find the first ordered pair by putting $x=4$ .
We put $x=4$ , in $y=6-1.25x$ we get –
$\begin{align}
  & \Rightarrow y=6-1.25\times 4 \\
 & =6-5 \\
 & =1 \\
\end{align}$
So, we get $y=1$ .
Hence for $x=4,y=1$
So first ordered pair is $\left( 4,1 \right)$ .
Now we put $x=0$ in $y=6-1.25x$ we get –
$\Rightarrow y=6-1.25\times 0$
By simplifying, we get –
$\begin{align}
  & y=6-0 \\
 & \Rightarrow y=0 \\
\end{align}$
So, we get for $x=0,y=6$ .
So, $\left( 0,6 \right)$ is the 2nd ordered pair.
Now we find another ordered pair by using $x=8$ .
We put $x=8$ in $y=6-1.25x$ , we get –
$\begin{align}
  & \Rightarrow y=6-1.25\times 8 \\
 & y=6-10 \\
\end{align}$
So, we get –
$\Rightarrow y=-4$
So for $x=8,y=-4$ .
So third ordered pair is $\left( 8,-4 \right)$
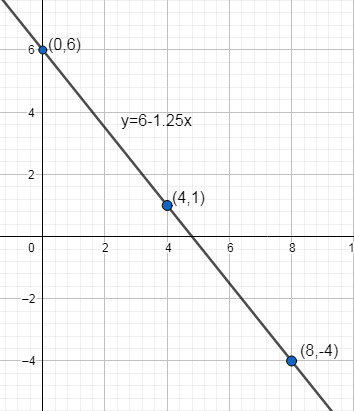
Now we get ordered pair as –
$\left( x,y \right)=\left( 4,1 \right),\left( 0,6 \right),\left( 8,-4 \right)$ .
Now we place them on a graph and join them.
The line form will be the graph of $y=6-1.25x$

Note: While solving problem we need to careful with calculator part like $6-2y=14$ here we cannot say $2y=14-6$ , we need to see that ‘2y’ has $\left( - \right)$ In front of it, we need to remove it. Another thing is that we should know dividing a positive term by a negative term will give us a negative term always, we can also find the graph by just finding the intercept of the graph and then joining them.