Question

How do you graph $y=5x-5$ ?

Answer 1

Hint: We are asked to draw the graph of the equation $y=5x-5$. The degree of an equation is the highest power of the variable present in it. So, as for this equation, the highest power present \[x\] is 1, the degree is also 1. From this, it can be said that this is a linear equation. The graph of a linear equation represents a straight line.

Complete step by step answer:
The general equation of a straight line is \[ax+by+c=0\], where \[a,b,c\] are any real numbers. The given equation is $y=5x-5$, the equation can also be written as \[5x-y-5=0\], comparing with the general equation of straight line, we get \[a=5,\,b=-1\And c=-5\].
To plot the graph of an equation of the straight line, we should know at least two points, through which the line passes.
To make things simple, let’s take the X-intercept and Y-intercept as the two points. X-intercept is the point where the line crosses X-axis, this means that the Y-coordinate will be \[0\], similarly Y-intercept is the point where the line crosses Y-axis, so X-coordinate will be \[0\]. We will use this property now.
We substitute \[y=0\] in the equation \[5x-y-5=0\], we get
\[\begin{align}
  & \Rightarrow 5x-(0)-5=0 \\
 & \Rightarrow 5x-5=0 \\
 & \Rightarrow 5x=5 \\
\end{align}\]
We divide both sides by 5, we get
\[\begin{align}
  & \Rightarrow \dfrac{5x}{5}=\dfrac{5}{5} \\
 & \therefore x=1 \\
\end{align}\]
So, the coordinates of the X-intercept are \[(1,0)\].
Similarly, now we substitute \[x=0\] in the equation \[5x-y-5=0\], we get
\[\Rightarrow 5\times 0-y-5=0\]
Adding \[y\] to both sides of the equation, we get
\[\begin{align}
  & \Rightarrow -y-5+y=y \\
 & \therefore y=-5 \\
\end{align}\]
So, the coordinates of the Y-intercept are \[(0,-5)\].
Using these two points we can plot the graph of the equation as follows:

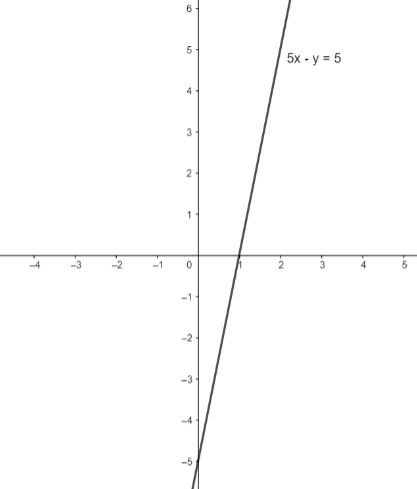
Note: Here, we found the two points which are X-intercept and Y-intercept by substituting either-or \[y\], one at a time. We can also find these values by converting the straight-line equation to the equation in intercept form which is, \[\dfrac{x}{a}+\dfrac{y}{b}=1\]. Here, \[a\And b\] are X-intercept and Y-intercept respectively.