
How do you graph $y=2x+3$?
Answer
531k+ views
Hint: We are given an equation $y=2x+3$, so we will learn about the type of equation and then depending on the type, we will learn what type of graph it should be. We will then find the point which would satisfy the given equation. To get the graph, we will plot those points on the graph and then join those points to get the required graph.
Complete step-by-step solution:
We have $y=2x+3$. We can see here that $x$ and $y$ are in linear scale since their power is $1$. Now we get that our function $y=2x+3$ is a linear function.
Linear function graph is a straight line. So, the graph of our equation $y=2x+3$ will also be a straight line. Now, to find the graph, we have to first find the point that satisfies this equation $y=2x+3$. To do so, we will consider the value of $x$ or $y$ by ourselves and then look for the corresponding value of $y$ or $x$.
Now as we have $y=2x+3$, we will take $x=1$.
We put $x=1$ in $y=2x+3$, so we get,
$\begin{align}
& y=2\times 1+3 \\
& \Rightarrow y=5 \\
\end{align}$
So for $x=1$, we have $y=5$
Similarly, we will find the other points also.
Let us consider $x=0$
So, putting $x=0$ in $y=2x+3$, we get,
$\begin{align}
& y=2\times 0+3 \\
& \Rightarrow y=3 \\
\end{align}$
So, for $x=0$, we have $y=3$
Now, let us consider another value too.
Let us consider $x=-1$
So, putting $x=-1$ in $y=2x+3$, we get,
$\begin{align}
& y=2\times \left( -1 \right)+3 \\
& \Rightarrow y=-2+3 \\
& \Rightarrow y=+1 \\
\end{align}$
So, for $x=-1$, we have $y=1$
Now we have got the points as,
Now, we will plot these points on the graph and join the points. The line thus obtained will be our graph of $y=2x+3$.
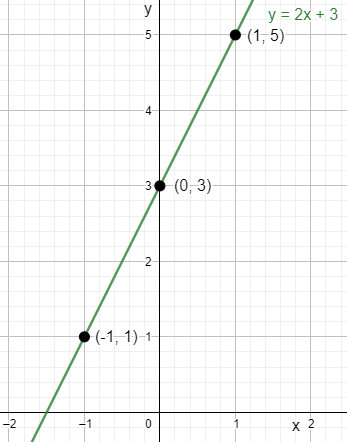
This is the graph of $y=2x+3$.
Note: Another way to graph this is to use the intercept. It means that to plot the graph, instead of finding the arbitrary points, we can just find the $x$ and $y$ intercept and plot the graph. To find the $x$ intercept, we put $y=0$ and solve for $x$ and to find the $y$ intercept, we put $x=0$ and solve for $y$.
Complete step-by-step solution:
We have $y=2x+3$. We can see here that $x$ and $y$ are in linear scale since their power is $1$. Now we get that our function $y=2x+3$ is a linear function.
Linear function graph is a straight line. So, the graph of our equation $y=2x+3$ will also be a straight line. Now, to find the graph, we have to first find the point that satisfies this equation $y=2x+3$. To do so, we will consider the value of $x$ or $y$ by ourselves and then look for the corresponding value of $y$ or $x$.
Now as we have $y=2x+3$, we will take $x=1$.
We put $x=1$ in $y=2x+3$, so we get,
$\begin{align}
& y=2\times 1+3 \\
& \Rightarrow y=5 \\
\end{align}$
So for $x=1$, we have $y=5$
Similarly, we will find the other points also.
Let us consider $x=0$
So, putting $x=0$ in $y=2x+3$, we get,
$\begin{align}
& y=2\times 0+3 \\
& \Rightarrow y=3 \\
\end{align}$
So, for $x=0$, we have $y=3$
Now, let us consider another value too.
Let us consider $x=-1$
So, putting $x=-1$ in $y=2x+3$, we get,
$\begin{align}
& y=2\times \left( -1 \right)+3 \\
& \Rightarrow y=-2+3 \\
& \Rightarrow y=+1 \\
\end{align}$
So, for $x=-1$, we have $y=1$
Now we have got the points as,
| $x$ | $-1$ | $0$ | $1$ |
| $y$ | $1$ | $3$ | $5$ |
Now, we will plot these points on the graph and join the points. The line thus obtained will be our graph of $y=2x+3$.

This is the graph of $y=2x+3$.
Note: Another way to graph this is to use the intercept. It means that to plot the graph, instead of finding the arbitrary points, we can just find the $x$ and $y$ intercept and plot the graph. To find the $x$ intercept, we put $y=0$ and solve for $x$ and to find the $y$ intercept, we put $x=0$ and solve for $y$.
Recently Updated Pages
Write a note about Jallianwala Bagh Tragedy class 10 social science CBSE

What is the relation between mean median and mode a class 10 maths CBSE

The bluish color of water in deep sea is due to A The class 10 physics CBSE

Distinguish between polar molecules and nonpolar m class 10 chemistry CBSE

Why did Frederic Sorrieu present utopian vision in class 10 social science CBSE

Describe the Mendels Law class 10 biology CBSE

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Which of the following does not have a fundamental class 10 physics CBSE

State and prove converse of BPT Basic Proportionality class 10 maths CBSE




