Question

How do you graph $y=-2x+10$ ?

Answer 1

Hint: In this question, we have to draw the graph of a given equation. The equation given to us consists of two variables, will we draw a two-dimensional graph. For drawing the graph, we have to use the substitution method to get the values of x and y, so that we can plot a graph. First, we put different values of x in the equation and solve for y. Similarly, we put different values of y in the equation and solve for x. Then, we plot those coordinates in the two-dimensional graph and join all the points to get a required curve or a straight line.

Complete step by step answer:
According to the question, it is given that equation is $y=-2x+10$ --------- (1)
We will apply the substitution method in the above equation, that is
Let x=0 in equation (1), we get
$\begin{align}
  & \Rightarrow y=-2(0)+10 \\
 & \Rightarrow y=0+10 \\
\end{align}$
Therefore, we get
$\Rightarrow y=10$
Thus, coordinate will become A(x,y)=A(0,10)
Let y=0 in equation (1), we get
$\Rightarrow 0=-2x+10$
Now, subtract 10 on both sides of the above equation, we get
$\Rightarrow 0-10=-2x+10-10$
As we know, the same terms with different signs cancel out each other, we get
$\Rightarrow -10=-2x$
Now, divide 2 on both sides of the equation, we get
$\begin{align}
  & \Rightarrow \dfrac{-10}{2}=\dfrac{-2}{2}x \\
 & \Rightarrow -5=-x \\
\end{align}$
Now, we will multiply (-1) on both sides in the above equation, we get
$\Rightarrow 5=x$
Thus, coordinate is B(x,y)=B(5,0)
 Let x=1 in equation (1), we get
$\begin{align}
  & \Rightarrow y=-2(1)+10 \\
 & \Rightarrow y=-2+10 \\
\end{align}$
Therefore, we get
$\Rightarrow y=8$
Thus, coordinate is C(x,y)=C(1,8)
Let y=1 in equation (1), we get
$\Rightarrow 1=-2x+10$
Now, subtract 10 on both sides in the above equation, we get
$\Rightarrow 1-10=-2x+10-10$
As we know, the same terms with different signs cancel out each other, we get
$\Rightarrow -9=-2x$
Now, divide 2 on both sides of the above equation, we get
$\begin{align}
  & \Rightarrow \dfrac{-9}{2}=\dfrac{-2}{2}x \\
 & \Rightarrow -4.5=-x \\
\end{align}$
Now, multiply (-1) on both sides of the equation, we get
$\Rightarrow -4.5.(-1)=-x.(-1)$
Therefore we get
$\Rightarrow 4.5=x$
Thus, coordinate is D(x,y)=D(4.5,1)
After finding these coordinates A(0,10), B(5,0), C(1,8), and D(4.5,1), we will plot these points on the graph, that is

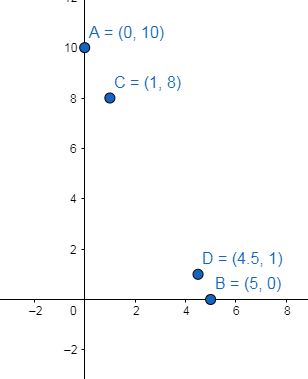
After plotting these points, join these points to get a curve of equation $y=-2x+10$ .

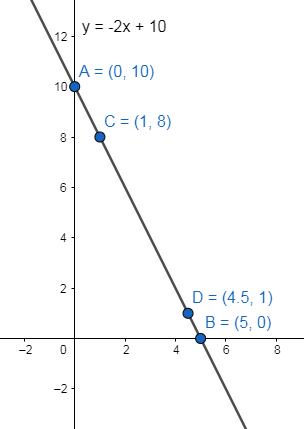
Therefore, for the equation $y=-2x+10$ , we have plotted the graph using different coordinates.

Note: Do all the calculations carefully to avoid calculation mistakes. For plotting the graph, atleast find 4 coordinates to get a perfect curve or a straight line. Always mention the points on the graph.