
How do you graph \[{y^2} = 9x\]?
Answer
540.6k+ views
Hint: To graph the given equation \[{y^2} = 9x\], as we can see that the given equation is a parabola with vertex at the origin i.e.,\[\left( {0,0} \right)\]. Hence, to graph the solution solve for y, and find the values of y with respect to x and then plot the graph and the obtained graph is a parabolic curve.
Complete step-by-step answer:
Let us write the given equation:
\[{y^2} = 9x\]
The given equation is a parabola with vertex at 0,0.
Let us solve the equation with respect to y as:
\[{y^2} = 9x\]
\[y = \pm \sqrt {9x} \]
As we have obtained the equation for y, now let us take 0 to 3 values for finding the values of x.
To graph the solution, solve one set of values for \[y = + \sqrt {9x} \] and another set of values for \[y = - \sqrt {9x} \] as we have obtained the equation of y as \[y = \pm \sqrt {9x} \].
When, \[y = + \sqrt {9x} \], the values of x and y are:
When, \[y = - \sqrt {9x} \], the values of x and y are:
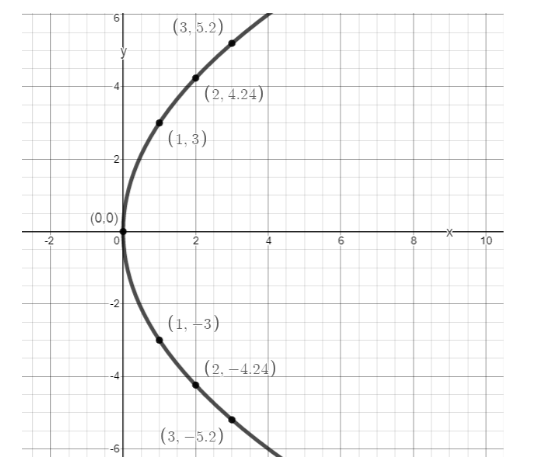
Now, let us plot the graph using the obtained values.
Note: To work with parabolas in the coordinate plane, we consider, those with the vertex at the origin and those with the vertex at appoint other than the origin, and to graph the given equation we must note the points with respect to \[y = + \sqrt {9x} \] and \[y = - \sqrt {9x} \] as x values of both the expressions remains same, hence we need to solve for y.
Complete step-by-step answer:
Let us write the given equation:
\[{y^2} = 9x\]
The given equation is a parabola with vertex at 0,0.
Let us solve the equation with respect to y as:
\[{y^2} = 9x\]
\[y = \pm \sqrt {9x} \]
As we have obtained the equation for y, now let us take 0 to 3 values for finding the values of x.
To graph the solution, solve one set of values for \[y = + \sqrt {9x} \] and another set of values for \[y = - \sqrt {9x} \] as we have obtained the equation of y as \[y = \pm \sqrt {9x} \].
When, \[y = + \sqrt {9x} \], the values of x and y are:
| x | y |
| 0 | 0.0 |
| 1 | 3.0 |
| 2 | 4.24 |
| 3 | 5.20 |
When, \[y = - \sqrt {9x} \], the values of x and y are:
| x | y |
| 0 | 0.0 |
| 1 | -3.0 |
| 2 | -4.24 |
| 3 | -5.20 |
Now, let us plot the graph using the obtained values.

Note: To work with parabolas in the coordinate plane, we consider, those with the vertex at the origin and those with the vertex at appoint other than the origin, and to graph the given equation we must note the points with respect to \[y = + \sqrt {9x} \] and \[y = - \sqrt {9x} \] as x values of both the expressions remains same, hence we need to solve for y.
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 English: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

Advantages and disadvantages of science

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE

What are the 12 elements of nature class 8 chemistry CBSE





