Question

How do you graph $y = - {x^2} - 4x + 2$?

Answer 1

Hint: Since the leading coefficient is negative, this quadratic equation will be downward parabola. Find the nature of its roots. If the equation has two distinct real roots then the graph will cut the $x - $ axis. Finally find the position of its vertex to identify whether it lies on the positive side or negative side of the $x - $axis.

Complete step-by-step answer:
According to the question, a quadratic equation is given to us and we have to show the process to draw its graph.
The given quadratic equation is:
$ \Rightarrow y = - {x^2} - 4x + 2$
Since its leading coefficient is negative, we know that its graph will be a downward parabola.
Nature of roots of a quadratic equation can be determined by its discriminant. For a quadratic equation $y = a{x^2} + bx + c$, the discriminant is $D = {b^2} - 4ac$.
$
   \Rightarrow D = {\left( { - 4} \right)^2} - 4 \times \left( { - 1} \right) \times 2 = 16 + 8 \\
   \Rightarrow D = 24 \\
 $
Determinant is positive means the equation has two distinct real roots. So the graph of this function will never cut the $x - $axis at two different points.
Till now we have the information that the graph will be a downward parabola cutting $x - $axis at two different points.
We still have to find the position of its vertex to identify whether it will lie on the positive side or negative side of the $x - $axis.
The $x - $coordinate of the vertex is calculated by differentiating its equation and putting it to zero. Doing so, we’ll get:
$
   \Rightarrow y = - {x^2} - 4x + 2 \\
   \Rightarrow \dfrac{{dy}}{{dx}} = - 2x - 4 \\
 $
Putting derivative to zero, we’ll get:
$
   \Rightarrow - 2x - 4 = 0 \\
   \Rightarrow x = - 2 \\
 $
Thus the vertex of the parabola will be at $x = - 2$.
Further, if we put $x = 0$ in the equation of the parabola, we have:
$
   \Rightarrow y\left( 0 \right) = - {\left( 0 \right)^2} - 4\left( 0 \right) + 2 \\
   \Rightarrow y\left( 0 \right) = 2 \\
 $
So the parabola will cut the $y - $ axis at $\left( {0,2} \right)$.
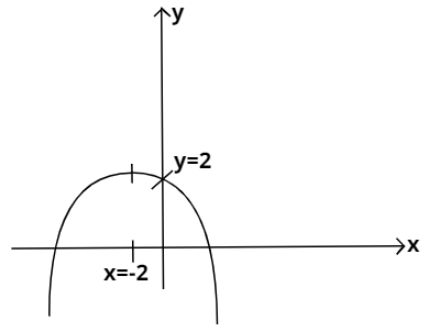
To conclude our observations of the graph of $y = - {x^2} - 4x + 2$, we have:
(1) The graph will be a downward parabola cutting $x - $ axis at two different points.
(2) Its vertex will be at a point where $x = - 2$.
(3) It will cut $y - $axis at $\left( {0,2} \right)$.
Based on these points, the graph can be drawn as shown below:

Note:
(1) If the leading coefficient of the parabola is positive the graph of the parabola will be opening upwards.
(2) If the discriminant of the quadratic equation is negative then the roots of the equation will be imaginary and the parabola will never cut or touch the $x - $axis.
(3) If the discriminant is positive then the parabola will cut the $x - $ axis and if the discriminant is zero then it will only touch the $x - $axis.