
How do you graph $y = {x^2} - 2x - 8$?
Answer
547.2k+ views
Hint: We have to find the properties of the given parabola. First rewrite the equation in vertex form. Next, use the vertex form of parabola, to determine the values of $a$, $h$, and $k$. Next, find the vertex and the distance from the vertex to the focus. Then, find the focus, axis of symmetry and directrix. Use the properties of the parabola to analyse and graph the parabola. Select a few $x$ values, and plug them into the equation to find the corresponding $y$ values. The $x$ values should be selected around the vertex. Graph the parabola using its properties and the selected points.
Formula used:
Vertex form of a parabola: $a{\left( {x + d} \right)^2} + e$
$d = \dfrac{b}{{2a}}$
$e = c - \dfrac{{{b^2}}}{{4a}}$
Vertex form: $y = a{\left( {x - h} \right)^2} + k$
Vertex: $\left( {h,k} \right)$
$p = \dfrac{1}{{4a}}$
Focus: $\left( {h,k + p} \right)$
Directrix: $y = k - p$
Complete step by step answer:
We have to find the properties of the given parabola.
So, first rewrite the equation in vertex form.
For this, complete the square for ${x^2} - 2x - 8$.
Use the form $a{x^2} + bx + c$, to find the values of $a$, $b$, and $c$.
$a = 1,b = - 2,c = - 8$
Consider the vertex form of a parabola.
$a{\left( {x + d} \right)^2} + e$
Now, substitute the values of $a$ and $b$ into the formula $d = \dfrac{b}{{2a}}$.
$d = \dfrac{{ - 2}}{{2 \times 1}}$
Simplify the right side.
$ \Rightarrow d = - 1$
Find the value of $e$ using the formula $e = c - \dfrac{{{b^2}}}{{4a}}$.
$e = - 8 - \dfrac{{{{\left( { - 2} \right)}^2}}}{{4 \times 1}}$
$ \Rightarrow e = - 9$
Now, substitute the values of $a$, $d$, and $e$ into the vertex form $a{\left( {x + d} \right)^2} + e$.
${\left( {x - 1} \right)^2} - 9$
Set $y$ equal to the new right side.
$y = {\left( {x - 1} \right)^2} - 9$
Now, use the vertex form, $y = a{\left( {x - h} \right)^2} + k$, to determine the values of $a$, $h$, and $k$.
$a = 1$
$h = 1$
$k = - 9$
Since the value of $a$ is positive, the parabola opens up.
Opens Up
Find the vertex $\left( {h,k} \right)$.
$\left( {1, - 9} \right)$
Now, find $p$, the distance from the vertex to the focus.
Find the distance from the vertex to a focus of the parabola by using the following formula.
$\dfrac{1}{{4a}}$
Substitute the value of $a$ into the formula.
$\dfrac{1}{{4 \times 1}}$
Multiply $4$ by $1$, we get
$ \Rightarrow \dfrac{1}{4}$
Find the focus.
The focus of a parabola can be found by adding $p$ to the $y$-coordinate $k$ if the parabola opens up or down.
$\left( {h,k + p} \right)$
Now, substitute the known values of $h$, $p$, and $k$ into the formula and simplify.
$\left( {1, - \dfrac{{35}}{4}} \right)$
Find the axis of symmetry by finding the line that passes through the vertex and the focus.
$x = 1$
Find the directrix.
The directrix of a parabola is the horizontal line found by subtracting $p$ from the $y$-coordinate $k$ of the vertex if the parabola opens up or down.
$y = k - p$
Now, substitute the known values of $p$ and $k$ into the formula and simplify.
$y = - \dfrac{{37}}{4}$
Use the properties of the parabola to analyse and graph the parabola.
Direction: Opens Up
Vertex: $\left( {1, - 9} \right)$
Focus: $\left( {1, - \dfrac{{35}}{4}} \right)$
Axis of Symmetry: $x = 1$
Directrix: $y = - \dfrac{{37}}{4}$
Select a few $x$ values, and plug them into the equation to find the corresponding $y$ values. The $x$ values should be selected around the vertex.
Replace the variable $x$ with $0$ in the expression.
\[f\left( 0 \right) = {0^2} - 2\left( 0 \right) - 8\]
Simplify the result.
\[f\left( 0 \right) = - 8\]
The final answer is $ - 8$.
The $y$ value at $x = 0$ is $ - 8$.
$y = - 8$
Replace the variable $x$ with $ - 1$ in the expression.
$f\left( { - 1} \right) = {\left( { - 1} \right)^2} - 2\left( { - 1} \right) - 8$
Simplify the result.
$f\left( { - 1} \right) = - 5$
The final answer is $ - 5$.
The $y$ value at $x = - 1$ is $ - 5$.
$y = - 5$
Replace the variable $x$ with $1$ in the expression.
$f\left( 1 \right) = {\left( 1 \right)^2} - 2\left( 1 \right) - 8$
Simplify the result.
$f\left( 1 \right) = - 9$
The final answer is $ - 9$.
The $y$ value at $x = 1$ is $ - 9$.
$y = - 9$
Replace the variable $x$ with $2$ in the expression.
\[f\left( 2 \right) = {\left( 2 \right)^2} - 2\left( 2 \right) - 8\]
Simplify the result.
\[f\left( 2 \right) = - 8\]
The final answer is $ - 8$.
The $y$ value at $x = 2$ is $ - 8$.
$y = - 8$
Replace the variable $x$ with $3$ in the expression.
\[f\left( 3 \right) = {\left( 3 \right)^2} - 2\left( 3 \right) - 8\]
Simplify the result.
\[f\left( 3 \right) = - 5\]
The final answer is $ - 5$.
The $y$ value at $x = 3$ is $ - 5$.
$y = - 5$
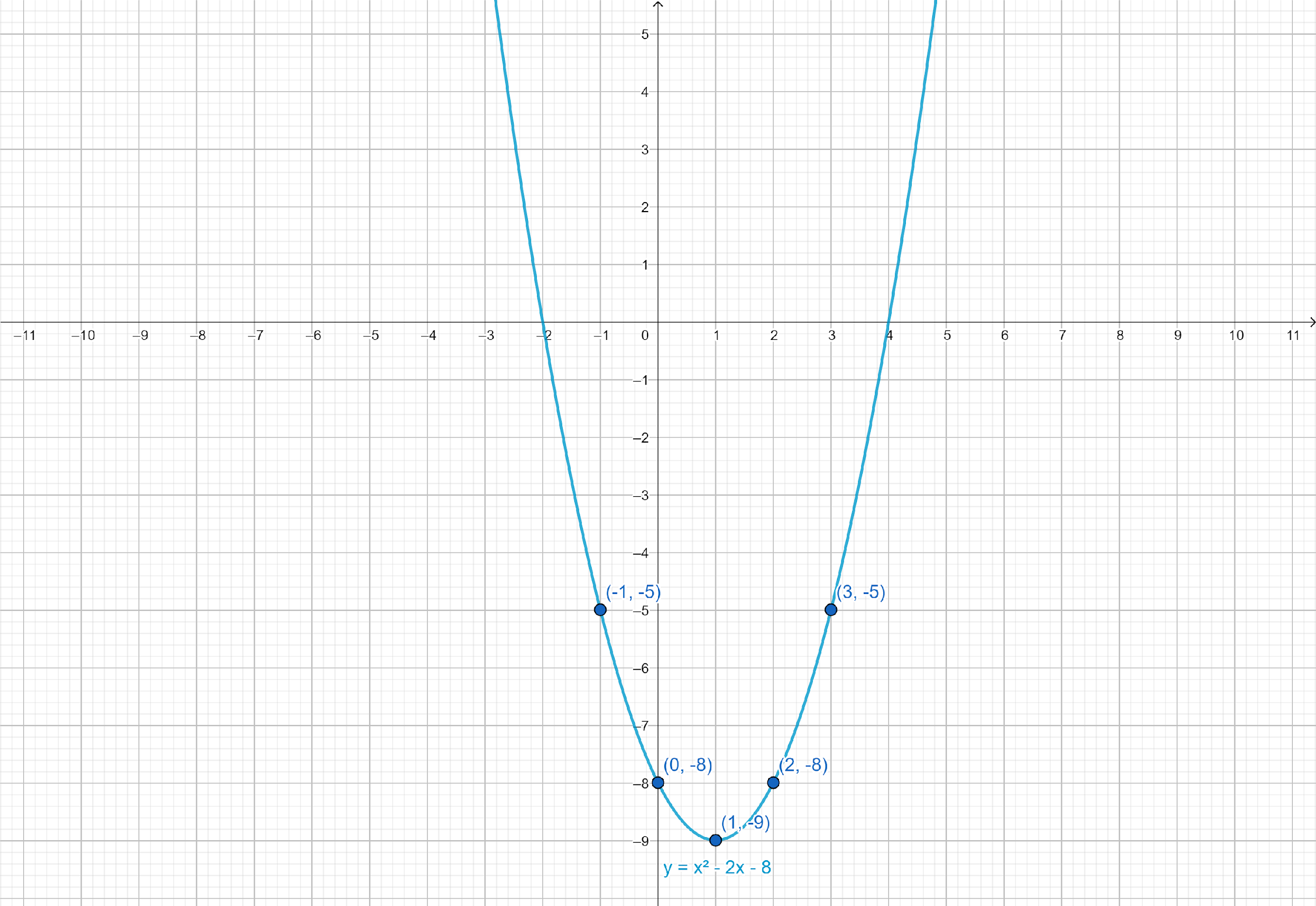
Graph the parabola using its properties and the selected points.
Direction: Opens Up
Vertex: $\left( {1, - 9} \right)$
Focus: $\left( {1, - \dfrac{{35}}{4}} \right)$
Axis of Symmetry: $x = 1$
Directrix: $y = - \dfrac{{37}}{4}$
Note: Vertex form of the quadratic function:
$y = a{\left( {x - h} \right)^2} + k$ where $\left( {h,k} \right)$ is the vertex or the “center” of the quadratic function or the parabola.
Formula used:
Vertex form of a parabola: $a{\left( {x + d} \right)^2} + e$
$d = \dfrac{b}{{2a}}$
$e = c - \dfrac{{{b^2}}}{{4a}}$
Vertex form: $y = a{\left( {x - h} \right)^2} + k$
Vertex: $\left( {h,k} \right)$
$p = \dfrac{1}{{4a}}$
Focus: $\left( {h,k + p} \right)$
Directrix: $y = k - p$
Complete step by step answer:
We have to find the properties of the given parabola.
So, first rewrite the equation in vertex form.
For this, complete the square for ${x^2} - 2x - 8$.
Use the form $a{x^2} + bx + c$, to find the values of $a$, $b$, and $c$.
$a = 1,b = - 2,c = - 8$
Consider the vertex form of a parabola.
$a{\left( {x + d} \right)^2} + e$
Now, substitute the values of $a$ and $b$ into the formula $d = \dfrac{b}{{2a}}$.
$d = \dfrac{{ - 2}}{{2 \times 1}}$
Simplify the right side.
$ \Rightarrow d = - 1$
Find the value of $e$ using the formula $e = c - \dfrac{{{b^2}}}{{4a}}$.
$e = - 8 - \dfrac{{{{\left( { - 2} \right)}^2}}}{{4 \times 1}}$
$ \Rightarrow e = - 9$
Now, substitute the values of $a$, $d$, and $e$ into the vertex form $a{\left( {x + d} \right)^2} + e$.
${\left( {x - 1} \right)^2} - 9$
Set $y$ equal to the new right side.
$y = {\left( {x - 1} \right)^2} - 9$
Now, use the vertex form, $y = a{\left( {x - h} \right)^2} + k$, to determine the values of $a$, $h$, and $k$.
$a = 1$
$h = 1$
$k = - 9$
Since the value of $a$ is positive, the parabola opens up.
Opens Up
Find the vertex $\left( {h,k} \right)$.
$\left( {1, - 9} \right)$
Now, find $p$, the distance from the vertex to the focus.
Find the distance from the vertex to a focus of the parabola by using the following formula.
$\dfrac{1}{{4a}}$
Substitute the value of $a$ into the formula.
$\dfrac{1}{{4 \times 1}}$
Multiply $4$ by $1$, we get
$ \Rightarrow \dfrac{1}{4}$
Find the focus.
The focus of a parabola can be found by adding $p$ to the $y$-coordinate $k$ if the parabola opens up or down.
$\left( {h,k + p} \right)$
Now, substitute the known values of $h$, $p$, and $k$ into the formula and simplify.
$\left( {1, - \dfrac{{35}}{4}} \right)$
Find the axis of symmetry by finding the line that passes through the vertex and the focus.
$x = 1$
Find the directrix.
The directrix of a parabola is the horizontal line found by subtracting $p$ from the $y$-coordinate $k$ of the vertex if the parabola opens up or down.
$y = k - p$
Now, substitute the known values of $p$ and $k$ into the formula and simplify.
$y = - \dfrac{{37}}{4}$
Use the properties of the parabola to analyse and graph the parabola.
Direction: Opens Up
Vertex: $\left( {1, - 9} \right)$
Focus: $\left( {1, - \dfrac{{35}}{4}} \right)$
Axis of Symmetry: $x = 1$
Directrix: $y = - \dfrac{{37}}{4}$
Select a few $x$ values, and plug them into the equation to find the corresponding $y$ values. The $x$ values should be selected around the vertex.
Replace the variable $x$ with $0$ in the expression.
\[f\left( 0 \right) = {0^2} - 2\left( 0 \right) - 8\]
Simplify the result.
\[f\left( 0 \right) = - 8\]
The final answer is $ - 8$.
The $y$ value at $x = 0$ is $ - 8$.
$y = - 8$
Replace the variable $x$ with $ - 1$ in the expression.
$f\left( { - 1} \right) = {\left( { - 1} \right)^2} - 2\left( { - 1} \right) - 8$
Simplify the result.
$f\left( { - 1} \right) = - 5$
The final answer is $ - 5$.
The $y$ value at $x = - 1$ is $ - 5$.
$y = - 5$
Replace the variable $x$ with $1$ in the expression.
$f\left( 1 \right) = {\left( 1 \right)^2} - 2\left( 1 \right) - 8$
Simplify the result.
$f\left( 1 \right) = - 9$
The final answer is $ - 9$.
The $y$ value at $x = 1$ is $ - 9$.
$y = - 9$
Replace the variable $x$ with $2$ in the expression.
\[f\left( 2 \right) = {\left( 2 \right)^2} - 2\left( 2 \right) - 8\]
Simplify the result.
\[f\left( 2 \right) = - 8\]
The final answer is $ - 8$.
The $y$ value at $x = 2$ is $ - 8$.
$y = - 8$
Replace the variable $x$ with $3$ in the expression.
\[f\left( 3 \right) = {\left( 3 \right)^2} - 2\left( 3 \right) - 8\]
Simplify the result.
\[f\left( 3 \right) = - 5\]
The final answer is $ - 5$.
The $y$ value at $x = 3$ is $ - 5$.
$y = - 5$
| $x$ | $y$ |
| $ - 1$ | $ - 5$ |
| $0$ | $ - 8$ |
| $1$ | $ - 9$ |
| $2$ | $ - 8$ |
| $3$ | $ - 5$ |
Graph the parabola using its properties and the selected points.
Direction: Opens Up
Vertex: $\left( {1, - 9} \right)$
Focus: $\left( {1, - \dfrac{{35}}{4}} \right)$
Axis of Symmetry: $x = 1$
Directrix: $y = - \dfrac{{37}}{4}$
| $x$ | $y$ |
| $ - 1$ | $ - 5$ |
| $0$ | $ - 8$ |
| $1$ | $ - 9$ |
| $2$ | $ - 8$ |
| $3$ | $ - 5$ |

Note: Vertex form of the quadratic function:
$y = a{\left( {x - h} \right)^2} + k$ where $\left( {h,k} \right)$ is the vertex or the “center” of the quadratic function or the parabola.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




