Question

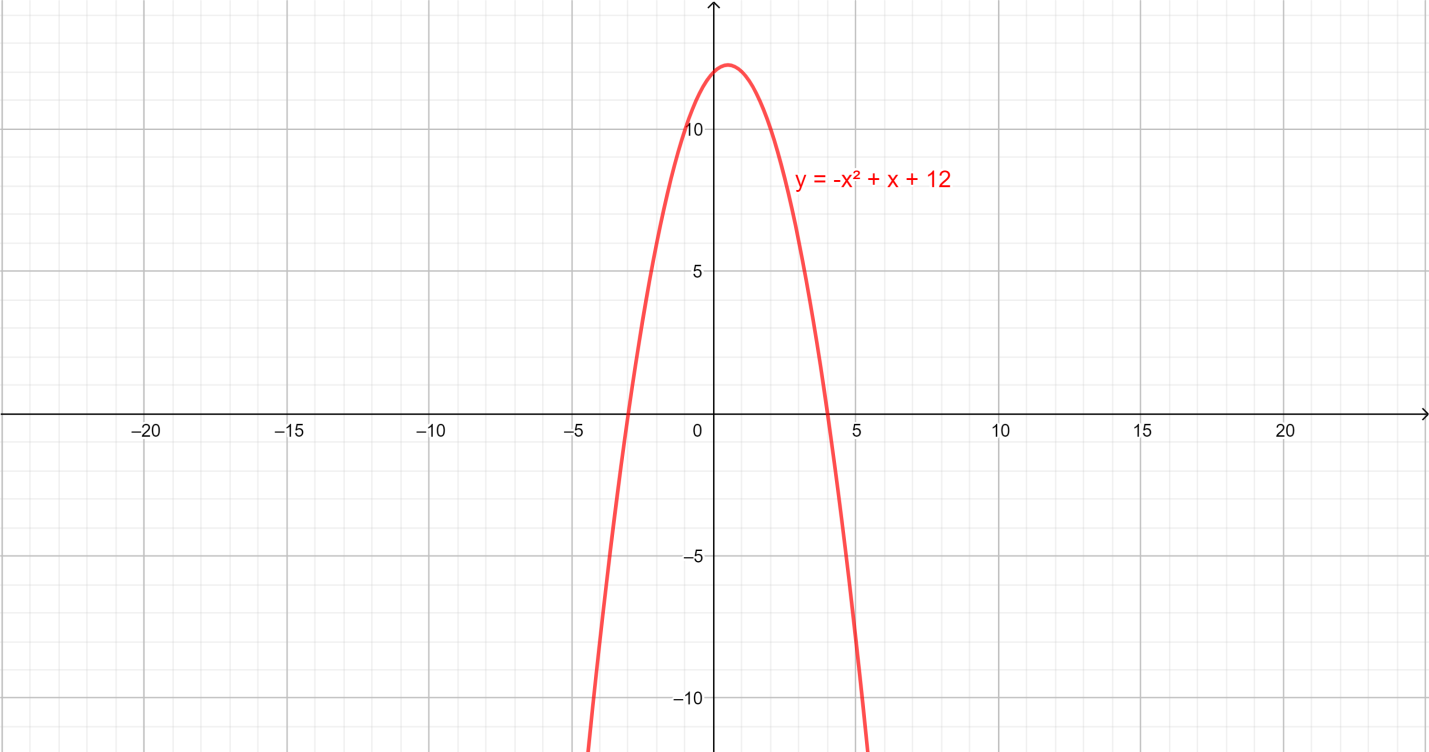
How do you graph $y = - {x^2} + x + 12$ ?

Answer 1

Hint: First we have to factorize the given expression. Then, we do some simplification; we will find the coordinates of the given equation and marked in the graph. Then we have to join the point to draw a graph of quadratic equations. Finally we get the required answer.

Complete step-by-step solution:
Here the given equation $y = - {x^2} + x + 12$ is a quadratic equation which is also known as parabola because there is an ${x^2}$ term.
Because the ${x^2}$ term is negative, we know the parabola is in the shape of a downwards.
First, to find out where the parabola crosses the $y$ axis, we set $x$ equal to $0$ and solve for $y$ :
$ \Rightarrow y = - {x^2} + x + 12$
Putting $x = 0$ we get,
$ \Rightarrow y = 0 + 0 + 12$
$ \Rightarrow y = 12$
The coordinate point is $A\left( {0,12} \right)$ .
Next, let’s find the two places where the graph intersects the $x$ axis. To do so, we set the function equal to $0$ and factor:
 $ \Rightarrow - {x^2} + x + 12 = 0$
Multiply $ - 1$ to both sides we get,
$ \Rightarrow {x^2} - x - 12 = 0$
Find the factor using factorization method we get,
\[\begin{array}{*{20}{c}}
  {\,\,\,\,\,\,\, - 12} \\
  {\,\,\,\, \swarrow - 1 \searrow } \\
  { - 4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,3}
\end{array}\]
Since $ - 4 + 3 = - 1\,\,,\,\,\left( { - 4} \right)\left( 3 \right) = - 12$
Therefore the factors are $ \Rightarrow {x^2} - x - 12 = \left( {x - 4} \right)\left( {x + 3} \right) = 0$
Hence the root is $x = 4\,\,,\,\,x = - 3$
There the coordinate point is $B\left( {4,0} \right)\,,\,\,C\left( { - 3,0} \right)$
So the parabola crosses the $x$ axis and $ - 3$ and $4$. Now we know three points for certain:
$\left( {0,12} \right)$ --where it crosses the $y$ axis.
$\left( {4,0} \right)$ --one of the $x$ axis crossing.
$\left( { - 3,0} \right)$ --other $x$ axis crossing.
So that should be enough information to draw the graph.

Note: A quadratic function has the general form $y = a{x^2} + bx + c$ represented graphically by a curve called parabola that has a shape of a downwards or upwards. The main features of this curve are:
Concavity: up or down. This depends upon the sign of the real number $a$
Vertex: the vertex is the highest or lowest point of the parabola.
Point of intercept with the $y$ axis this is the point where the crosses the $y$ axis and has coordinates:$\left( {0,c} \right)$
Possible points of intercept with the $x$ axis. These are the points where the parabola crosses the $x$ axis.
They are obtained by putting $y = 0$ and solving for $x$ the second degree equation: $a{x^2} + bx + c = 0$, which will give the $x$ coordinates of these points. Depending on the discriminant $\Delta = {b^2} - 4ac$ if it is $ < 0$ the parabola does not cross the $x$ axis.