
How do you graph $ y = {x^2} + 1 $ ?
Answer
563.1k+ views
Hint: To graph the above equation find the turning point of the parabola by putting $ x = 0 $ and find some ordered pairs and reflect them on the graph to obtain the desired parabola.
Complete step-by-step answer:
Given a equation $ y = {x^2} + 1 $ -(1)
Since We’ve given a x squared equation so the graph to the equation is no longer a straight line. In this case it is quadratic as x is raised to the power 2 .
So, we expect the graph of this equation to look like a parabola.
First we’ll find the turning point of the graph .So to find the turning point of the graph put
$
{x^2} = 0 \\
x = 0 \;
$
Now substituting the x in equation (1)
$
y = {0^2} + 1 \\
y = 1 \;
$
So our turning point is when x equals 0 and y equal to 1 when our parabola start turning into opposite direction.
Let’s find some of the ordered pairs that we will plot on the graph on one side of the turning point
Since we have the turning point of the parabola we can simply reflect these ordered pair in order to get our full parabola .
Therefore , above is the above to the equation $ y = {x^2} + 1 $
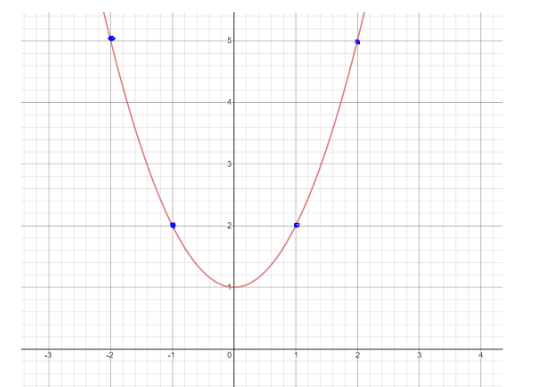
Note: 1. Cartesian Plane: A Cartesian Plane is given its name by the French mathematician Rene Descartes ,who first used this plane in the field of mathematics .It is defined as the two mutually perpendicular number line , the one which is horizontal is given name x-axis and the one which is vertical is known as y-axis. With the help of these axes we can plot any point on this cartesian plane with the help of an ordered pair of numbers.
2.Draw the cartesian plane only with the help of a straight ruler and pencil to get the perfect and accurate results.
Complete step-by-step answer:
Given a equation $ y = {x^2} + 1 $ -(1)
Since We’ve given a x squared equation so the graph to the equation is no longer a straight line. In this case it is quadratic as x is raised to the power 2 .
So, we expect the graph of this equation to look like a parabola.
First we’ll find the turning point of the graph .So to find the turning point of the graph put
$
{x^2} = 0 \\
x = 0 \;
$
Now substituting the x in equation (1)
$
y = {0^2} + 1 \\
y = 1 \;
$
So our turning point is when x equals 0 and y equal to 1 when our parabola start turning into opposite direction.
Let’s find some of the ordered pairs that we will plot on the graph on one side of the turning point
| X | 1 | 2 |
| y | 2 | 5 |
Since we have the turning point of the parabola we can simply reflect these ordered pair in order to get our full parabola .
Therefore , above is the above to the equation $ y = {x^2} + 1 $

Note: 1. Cartesian Plane: A Cartesian Plane is given its name by the French mathematician Rene Descartes ,who first used this plane in the field of mathematics .It is defined as the two mutually perpendicular number line , the one which is horizontal is given name x-axis and the one which is vertical is known as y-axis. With the help of these axes we can plot any point on this cartesian plane with the help of an ordered pair of numbers.
2.Draw the cartesian plane only with the help of a straight ruler and pencil to get the perfect and accurate results.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
Difference Between Plant Cell and Animal Cell

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Which places in India experience sunrise first and class 9 social science CBSE

Who is eligible for RTE class 9 social science CBSE

What is pollution? How many types of pollution? Define it

Name 10 Living and Non living things class 9 biology CBSE





