Question

How do you graph \[y = \sin \left( {3x} \right)\]?

Answer 1

Hint: Here, we will draw the graph for the given trigonometric function. We will find the amplitude, phase shift, period, and vertical shift by using the condition of a sinusoidal function. Thus, by using the period, we will find the coordinates of x and by using the coordinates of x, we will find the coordinates of y. Thus, by plotting the coordinates, we will plot the graph. Thus, the graph of the trigonometric equation is the required answer.

Formula Used:
We will use the following formula:
1. Period of the function is given by the formula Period \[= \dfrac{{2\pi }}{{\left| \omega \right|}}\]
2. The phase shift is given by the formula Phase shift \[= \dfrac{\phi }{\omega }\]

Complete step by step solution:
We are given an equation\[y = \sin \left( {3x} \right)\].
We know that the sinusoidal function graph is of the form \[f\left( x \right) = a\sin \left( {\omega x - \phi } \right) + k\]. But it is not necessary to have \[\left( { - \phi } \right) + k\].
The given equation \[y = \sin \left( {3x} \right)\] is of the form\[f\left( x \right) = a\sin \left( {\omega x - \phi } \right) + k\] where \[a,\omega ,\phi ,k\] are used to find the amplitude, period, Phase shift and vertical shift.
So, we get \[f\left( x \right) = y\];\[a = 1;\]\[\omega = 3;\]\[\phi = 0\] and\[k = 0\]
\[ \Rightarrow Amplitude = 1\]
Period of the function is given by the formula \[Period = \dfrac{{2\pi }}{{\left| \omega \right|}}\]
By substituting \[\omega = 3\] in the Period formula, we get
\[ \Rightarrow Period = \dfrac{{2\pi }}{{\left| 3 \right|}}\]
\[ \Rightarrow Period = \dfrac{{2\pi }}{3}\]
The phase shift is given by the formula \[Phase{\rm{ }}Shift = \dfrac{\phi }{\omega }\]
By substituting \[\omega = 3,\phi = 0\] in the Phase shift formula, we get
\[ \Rightarrow Phase{\rm{ }}Shift = \dfrac{0}{3}\]
\[ \Rightarrow Phase{\rm{ }}Shift = 0\]
\[ \Rightarrow Vertical{\rm{ }}Shift = 0\]
Now, we will find the four coordinates of \[x\], which is half of the consecutive periods.
\[ \Rightarrow \] First Point\[ = \dfrac{{\dfrac{{2\pi }}{3}}}{2}\]
\[ \Rightarrow \] First Point\[ = \dfrac{\pi }{3}\]
\[ \Rightarrow \] Second Point\[ = \dfrac{{\dfrac{\pi }{3}}}{2}\]
\[ \Rightarrow \] Second Point\[ = \dfrac{\pi }{6}\]
Let the coordinates of \[x\] be \[0,\dfrac{\pi }{6},\dfrac{\pi }{3},\dfrac{\pi }{2},\dfrac{{2\pi }}{3}\].
Now, we will find the coordinates of \[y\] by using the given equation.
Substituting \[x = 0\] in the given equation, we get
\[ \Rightarrow f\left( 0 \right) = \sin \left( {3\left( 0 \right)} \right)\]
\[ \Rightarrow f\left( 0 \right) = \sin \left( {\left( 0 \right)} \right) = 0\]
Substituting \[x = \dfrac{\pi }{6}\] in the given equation, we get
\[ \Rightarrow f\left( {\dfrac{\pi }{6}} \right) = \sin \left( {3\left( {\dfrac{\pi }{6}} \right)} \right)\]
\[ \Rightarrow f\left( {\dfrac{\pi }{6}} \right) = \sin \left( {\dfrac{\pi }{2}} \right) = 1\]
Substituting\[x = \dfrac{\pi }{3}\] in the given equation, we get
\[ \Rightarrow f\left( {\dfrac{\pi }{3}} \right) = \sin \left( {3\left( {\dfrac{\pi }{3}} \right)} \right)\]
\[ \Rightarrow f\left( {\dfrac{\pi }{3}} \right) = \sin \left( \pi \right) = 0\]
Substituting \[x = \dfrac{\pi }{2}\] in the given equation, we get
\[ \Rightarrow f\left( {\dfrac{\pi }{2}} \right) = \sin \left( {3\left( {\dfrac{\pi }{2}} \right)} \right) = \sin \left( {\dfrac{{3\pi }}{2}} \right)\]
\[ \Rightarrow f\left( {\dfrac{\pi }{2}} \right) = \sin \left( {2\pi - \dfrac{\pi }{2}} \right) = - \sin \left( {\dfrac{\pi }{2}} \right)\] since \[\sin \left( {\dfrac{{3\pi }}{2}} \right)\] lies in the fourth quadrant.
\[ \Rightarrow f\left( {\dfrac{\pi }{2}} \right) = - 1\]
Substituting \[x = \dfrac{{2\pi }}{3}\] in the given equation, we get
\[ \Rightarrow f\left( {\dfrac{{2\pi }}{3}} \right) = \sin \left( {3\left( {\dfrac{{2\pi }}{3}} \right)} \right) = \sin \left( {2\pi } \right)\]
\[ \Rightarrow f\left( {\dfrac{{2\pi }}{3}} \right) = \sin \left( 0 \right)\]
\[ \Rightarrow f\left( {\dfrac{{2\pi }}{3}} \right) = 0\]
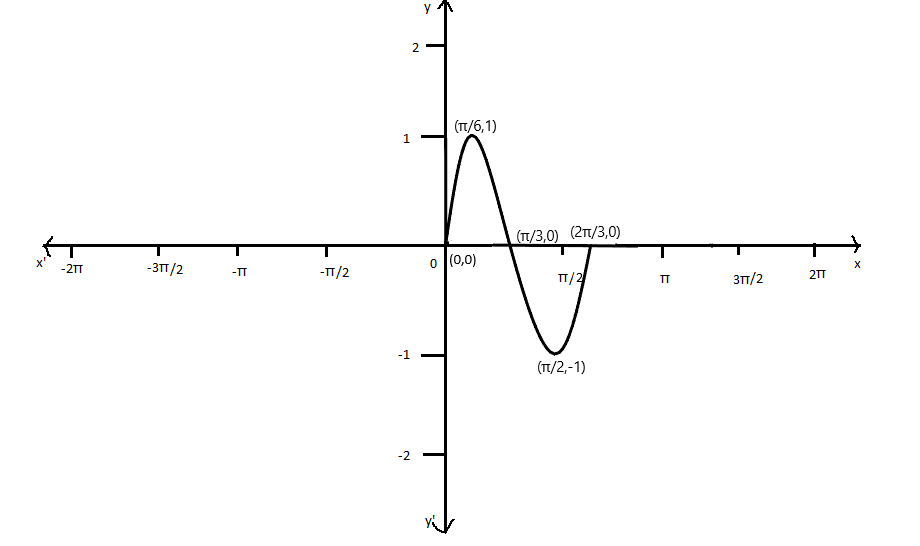
The coordinates of the function \[y = \sin 3x\] are \[\left( {0,0} \right)\],\[\left( {\dfrac{\pi }{6},1} \right)\] ,\[\left( {\dfrac{\pi }{3},0} \right)\] ,\[\left( {\dfrac{\pi }{2}, - 1} \right)\], \[\left( {\dfrac{{2\pi }}{3},0} \right)\]
Now, we will plot the coordinates for the function in a graph, we get y=sin(3x)

Note:
We know that Trigonometric Equation is defined as an equation involving trigonometric ratios. Trigonometric identity is an equation that is always true for all the variables. We should remember the rules that all the Trigonometric Ratios are positive in the First Quadrant. Sine and Cosecant are positive in the second quadrant and the rest are negative. Tangent and Cotangent are positive in the third quadrant and the rest are negative. Cosine and Secant are positive in the fourth quadrant and the rest are negative. This can be remembered as the ASTC rule in Trigonometry. This rule is used in determining the signs of the trigonometric ratio.