Question

How do you graph $y = {\log _2}(x - 1) + 3$?

Answer 1

Hint: In this question we have logarithmic function; we will compare this function to the general logarithmic function and make the graph for it.

Complete step-by-step solution:
We have the given logarithmic function as:
$y = {\log _2}(x - 1) + 3$
We know the range of the logarithmic function is $x \in \mathbb{R}$, which means that the function is defined to all the real numbers which are present in the $Y$ axis.
In this question, the domain is trickier, the asymptote of the equation will be considered.
A normal asymptote will occur when we write ${\log _2}0 = \dfrac{{\log 0}}{{\log 2}}$ appears. This is the same case just like in rational functions.
We can determine the equations of any asymptotes by setting the value of the function as $0$.
For this question, we will consider $x - 1$ because it is contained by a logarithm of base $2$.
Therefore, we get:
$x - 1 = 0$
On rearranging the terms, we get:
$x = 1$
Therefore, in this case the asymptote will be a vertical asymptote at $x = 1$.
Now we will find the reflections, stretches, compressions and vertical or horizontal transformations in the given equation.
We will find the transformations when we convert the general function $y = {\log _2}x$ to the function $y = \log (x - 1) + 3$
We have calculated that there is a horizontal transformation of $1$ unit to the right, and since $3$ is added to the function, there will be a vertical transformation of $3$ units upwards.
Now that we know the transformations, we can plot the graph as:

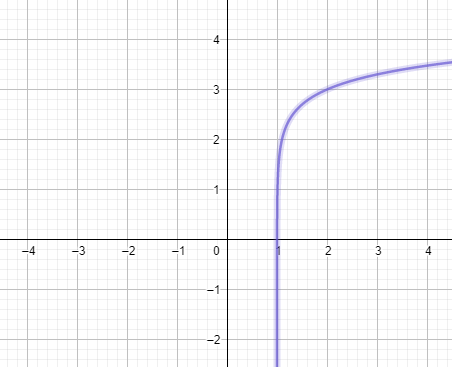
Which is the required graph to the function.

Note: Logarithm is used to simplify a mathematical expression, it converts multiplication to addition, division to subtraction and exponents to multiplication.
The most commonly used bases in logarithm are $10$ and $e$ which has a value of approximate $2.713...$