Question

How do you graph $ y = \dfrac{x}{2} + 3 $ ?

Answer 1

Hint: In this question we are supposed to find the graph of the given equation $ y = \dfrac{x}{2} + 3 $ . The given equation is linear in order with respect to both variables $ x $ and $ y $ . To plot the graph of this equation we will first find some point i.e., pairs of $ x,y $ such that they satisfy the given equation. Then we will place these points on the X-Y plane.

Complete step-by-step solution:
In this question we need to plot the graph of equation $ y = \dfrac{x}{2} + 3 $ . To plot this equation we will first find that this equation is of line, circle or some other 2-D shapes. Since our given equation is of linear order in both the variables, so it can be the equation of a line. Because the equation of a straight line is of the form $ y = mx + c $ and our equation is $ y = \dfrac{x}{2} + 3 $ .
In our equation we have $ m = \dfrac{1}{2} $ and $ c = 3 $ . Since the given equation $ y = \dfrac{x}{2} + 3 $ is of a straight line.
Now, we will find some point which lies on the given equation by putting the value of $ x $ and $ y $ respectively.
$ y = \dfrac{x}{2} + 3 $ $ eq(1) $

Let us take $ x = 0 $ then value of $ x $ in $ eq(1) $ , we get $ y = 3 $ .
Similarly, Let us take $ x = 1 $ then value of $ x $ in $ eq(1) $ , we get $ y = \dfrac{7}{2} $ .
Similarly, Let us take $ x = 2 $ then the value of $ x $ in $ eq(1) $ , we get $ y = 4 $ .
Similarly, Let us take $ x = - 1 $ then value of $ x $ in $ eq(1) $ , we get $ y = \dfrac{5}{2} $ .
Similarly, Let us take $ x = - 2 $ then value of $ x $ in $ eq(1) $ , we get $ y = 2 $ .Now we have some points which lies on $ y = \dfrac{x}{2} + 3 $ , here is the graph

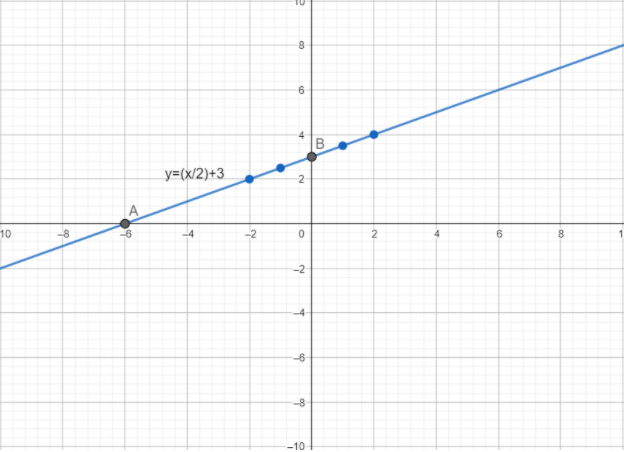
These blue dots are the above points which we find by assuming the value of $ x $


Note: To check whether your graph is correct or not just take any point from the line put in the given equation, if it satisfies then your plotted graph is correct. For example: $(6,6)$ is a point on the line. Putting $(6,6)$ in the equation$y = \dfrac{x}{2} + 3$, we get
$
  6 = \dfrac{6}{2} + 3 \\
  6 = 3 + 3 \\
  6 = 6 \\
  LHS = RHS \\
 $
Hence the plotted graph of equation$y = \dfrac{x}{2} + 3$ is correct.