Question

How do you graph $ y = \dfrac{4}{3}x + 2 $ ?

Answer 1

Hint: A graph shows the relation between two variable quantities, it contains two axes perpendicular to each other namely the x-axis and the y-axis. Each variable is measured along one of the axes. In the question, we are given one linear equation containing two variables namely x and y, x is measured along the x-axis and y is measured along the y-axis while tracing the given equations. To find the equation of a line, we must know the coordinates of at least two of the points lying on the line. We are given the equation of a line in the question so we have to find the coordinates using the given equation and then plot its graph.

Complete step-by-step answer:
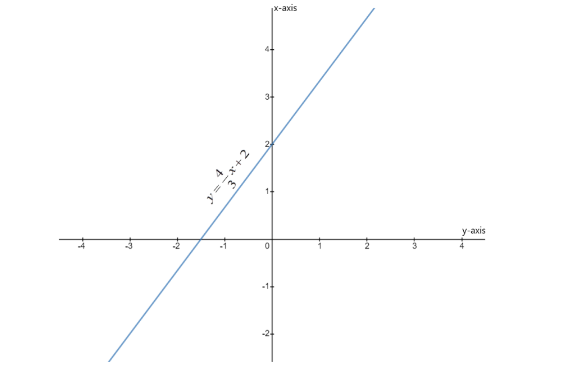
The equation of the line is \[y = \dfrac{4}{3}x + 2\]
When $ x = 0 $
\[
  y = \dfrac{4}{3}(0) + 2 \\
   \Rightarrow y = 2 \;
 \]
The line cuts the y-axis at $ (0,2) $ .
When $ y = 0 $
\[
  0 = \dfrac{4}{3}x + 2 \\
   \Rightarrow x = - \dfrac{3}{2} \;
 \]
The line cuts the x-axis at the point $ ( - \dfrac{3}{2},0) $ .
We can trace the line of the equation \[y = \dfrac{4}{3}x + 2\] by joining these two points and then extending the obtained line away in the opposite directions.

Note: We are given a linear equation in terms of two variable quantities namely x and y and we have to graph it. On putting random values of x, we can get random values of y and thus find the coordinates of one of the points lying on the line. To plot the graph of a straight line we must know the coordinates of at least two points lying on the line so we can put any random values of x and y. We put the value of both x and y zero one by one and then find the value of other variables from the equation of the line.