Question

How do you graph $y = \dfrac{1}{{x - 2}}?$

Answer 1

Hint: First find where the right hand side expression is not defined, then draw the graph of $y = \dfrac{1}{x}$ and shift it to two units on the right side. You will get the required graph of the equation.

Complete step by step answer:
In order to draw the graph of the equation $y = \dfrac{1}{{x - 2}}$, we will first find where the expression $\dfrac{1}{{x - 2}}$ is not defined, since the expression is in fraction, and a fraction is not defined only when its denominator equals zero,
$\Rightarrow x - 2 = 0 \\
\Rightarrow x = 2 $
That is the function is not defined at $x = 2$.Now to draw the graph of $y = \dfrac{1}{{x - 2}}$ we will first draw the graph of $y = \dfrac{1}{x}$ as follows
Consider a rational function $F(x) = \dfrac{{a{x^m}}}{{b{x^n}}},\;{\text{where}}\;m\;{\text{and}}\;n$ are degrees of numerator and denominator respectively.
Now,
-If $m < n,$ then the x-axis, $y = 0$, is the horizontal asymptote.
-If $m = n,$ then the line $y = \dfrac{a}{b}$ is the horizontal asymptote.
-And if $m > n,$ there is an oblique asymptote, no horizontal asymptote.
In the function $y = \dfrac{1}{x}$ value of $m\;{\text{and}}\;n$ are $0\;{\text{and}}\;1$ respectively.Therefore the x-axis, $y = 0$ is the horizontal asymptote and no oblique asymptote because $m < n,$
So in the graph of $y = \dfrac{1}{x}$,
Following asymptotes are there
Horizontal asymptote: $y = 0$
Vertical asymptote: $x = 0$
And, no oblique asymptote
So the graph of $y = \dfrac{1}{x}$ will be as follows

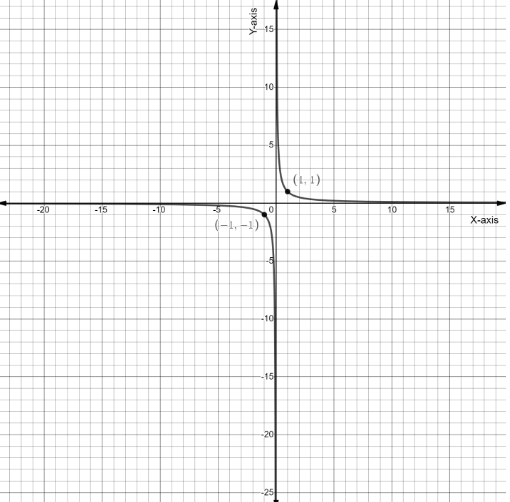
Now to draw the required graph of equation $y = \dfrac{1}{{x - 2}}$, we will shift the graph of $y = \dfrac{1}{x}$ to two unit right side, so the required graph will look as follows

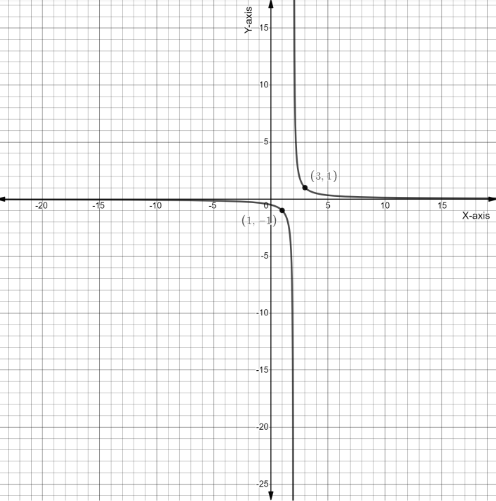
This is the required graph of equation $y = \dfrac{1}{{x - 2}}$

Note:Graph should not touch the x-axis or the line $y = 2$ because both are the asymptote of $y = \dfrac{1}{{x - 2}}$. We have shifted the graph of $y = \dfrac{1}{x}$ two unit right side to get required graph because if function $f(x)$ and we want to draw graph of $f(x \pm a)$ then we shift the graph of $f(x)$ to $a$ units right or left side according to $ + \;or\; - $ sign.