
How do you graph $ y = \dfrac{1}{{\sin x}} $ ?
Answer
530.1k+ views
Hint: In order to graph the above trigonometric function, first rewrite the function as $ y = \csc x $ as both are the same. Now draft some of the properties of the cosecant ,i.e. amplitude, period, period shift, vertical shift by finding the value of variable by comparing with the standard form of cosecant function i.e. $ a\csc \left( {bx - c} \right) + d $ . Find some few point of the function by putting $ x = \dfrac{\pi }{2},\dfrac{{3\pi }}{2},\dfrac{{5\pi }}{2},\dfrac{{7\pi }}{2},\dfrac{{9\pi }}{2} $ to obtain the required graph.
Complete step by step solution:
We are given a trigonometric function i.e. $ y = \dfrac{1}{{\sin x}} $
As we know that the reciprocal of sine function is nothing but the cosecant function , so we can write the above function as
$ y = \csc x $
In order to graph the above function , we have to find out the asymptotes , amplitude, period , phase shift and vertical shift
Vertical asymptotes of secant and cosecant function exist but there are no horizontal asymptotes of these functions.
Vertical asymptote of $ \csc x $ : $ x = \pi n $ where n is any integer
Comparing the $ \csc x $ with the standard form of $ \csc x $ i.e. $ a\csc \left( {bx - c} \right) + d $ to find the variables. These values of variables will help us to find the amplitude, period, phase shift and vertical shift.
a=1
b=1
c=0
d=0
The function does not have any minimum or maximum value so there is no value for Amplitude
Period: $ \dfrac{{2\pi }}{{\left| b \right|}} = \dfrac{{2\pi }}{1} = 2\pi $
Phase shift is the ratio of $ c\,and\,d $ i.e. $ = \dfrac{c}{d} = 0 $
Vertical shift $ = d = 0 $
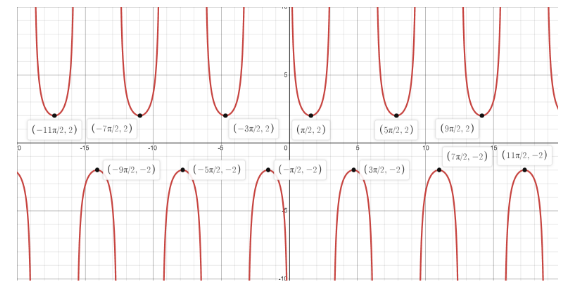
Let's find some few point by putting values of $ x = \dfrac{\pi }{2},\dfrac{{3\pi }}{2},\dfrac{{5\pi }}{2},\dfrac{{7\pi }}{2},\dfrac{{9\pi }}{2} $
Lets obtain the graph with the point above and the properties of cosecant function
Amplitude =Null
Period: $ = 2\pi $
Phase shift $ = 0 $
Vertical shift $ = 0 $
Note: 1.Draw the cartesian plane only with the help of straight ruler and pencil to get the perfect and accurate results.
2.Mark the points carefully.
3. x-intercept is the point at which the line intersects the x-axis of the plane and similarly y-intercept is the point at which line intersects the y-axis of the plane.
4. In this question, we have used trigonometry. Trigonometry is a branch of mathematics that helps us to study the relationship between the sides and the angles of a triangle. In practical life, trigonometry is used to make maps). It is also used by the aviation and naval industries.
Complete step by step solution:
We are given a trigonometric function i.e. $ y = \dfrac{1}{{\sin x}} $
As we know that the reciprocal of sine function is nothing but the cosecant function , so we can write the above function as
$ y = \csc x $
In order to graph the above function , we have to find out the asymptotes , amplitude, period , phase shift and vertical shift
Vertical asymptotes of secant and cosecant function exist but there are no horizontal asymptotes of these functions.
Vertical asymptote of $ \csc x $ : $ x = \pi n $ where n is any integer
Comparing the $ \csc x $ with the standard form of $ \csc x $ i.e. $ a\csc \left( {bx - c} \right) + d $ to find the variables. These values of variables will help us to find the amplitude, period, phase shift and vertical shift.
a=1
b=1
c=0
d=0
The function does not have any minimum or maximum value so there is no value for Amplitude
Period: $ \dfrac{{2\pi }}{{\left| b \right|}} = \dfrac{{2\pi }}{1} = 2\pi $
Phase shift is the ratio of $ c\,and\,d $ i.e. $ = \dfrac{c}{d} = 0 $
Vertical shift $ = d = 0 $
Let's find some few point by putting values of $ x = \dfrac{\pi }{2},\dfrac{{3\pi }}{2},\dfrac{{5\pi }}{2},\dfrac{{7\pi }}{2},\dfrac{{9\pi }}{2} $
| x | $ f\left( x \right) $ |
| $ \dfrac{\pi }{2} $ | 1 |
| $ \dfrac{{3\pi }}{2} $ | -1 |
| $ \dfrac{{5\pi }}{2} $ | 1 |
| $ \dfrac{{7\pi }}{2} $ | -1 |
| $ \dfrac{{9\pi }}{2} $ | 1 |
Lets obtain the graph with the point above and the properties of cosecant function
Amplitude =Null
Period: $ = 2\pi $
Phase shift $ = 0 $
Vertical shift $ = 0 $

Note: 1.Draw the cartesian plane only with the help of straight ruler and pencil to get the perfect and accurate results.
2.Mark the points carefully.
3. x-intercept is the point at which the line intersects the x-axis of the plane and similarly y-intercept is the point at which line intersects the y-axis of the plane.
4. In this question, we have used trigonometry. Trigonometry is a branch of mathematics that helps us to study the relationship between the sides and the angles of a triangle. In practical life, trigonometry is used to make maps). It is also used by the aviation and naval industries.
Recently Updated Pages
Why are manures considered better than fertilizers class 11 biology CBSE

Find the coordinates of the midpoint of the line segment class 11 maths CBSE

Distinguish between static friction limiting friction class 11 physics CBSE

The Chairman of the constituent Assembly was A Jawaharlal class 11 social science CBSE

The first National Commission on Labour NCL submitted class 11 social science CBSE

Number of all subshell of n + l 7 is A 4 B 5 C 6 D class 11 chemistry CBSE

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE




