Question

How do you graph $ y = \dfrac{1}{4} + \sin x $ ?

Answer 1

Hint:This question deals with the properties of $ \sin $ . Here we will use different characteristics of the trigonometric function.
 $ \sin $ function is a periodic function with a period of $ 2\pi $ .the domain of $ \sin $ function is defined in the interval of $ \left( { - \infty ,\infty } \right) $ and the range of $ \sin $ function is $ \left[ { - 1,1} \right] $ . $ \sin $ is an odd function which means its graph will be symmetric about origin.an odd function is defined as a function which is symmetric about the origin. The mathematical expression for odd function is defined as $ f\left( { - x} \right) + f\left( x \right) = 0 $ ,the $ x - $ intercept of $ \sin $ function is $ k\pi $ ,where $ k $ is an integer and the $ y - $ intercept of the function is 0.the maximum points of the function are $ \left( {\dfrac{\pi }{2} + 2k\pi ,1} \right) $ where $ k $ is an integer and the minimum points of the function are $ \left( {\dfrac{{3\pi }}{2} + 2k\pi , - 1} \right) $ where $ k $ is an integer.
The function over one period and from 0 to $ 2\pi $ is increasing in the interval $ \left( {0,\dfrac{\pi }{2}} \right) $ and $ \left( {\dfrac{{3\pi }}{2},2\pi } \right) $ ,and decreasing in the interval $ \left( {\dfrac{\pi }{2},\dfrac{{3\pi }}{2}} \right) $ .

Complete step by step answer:
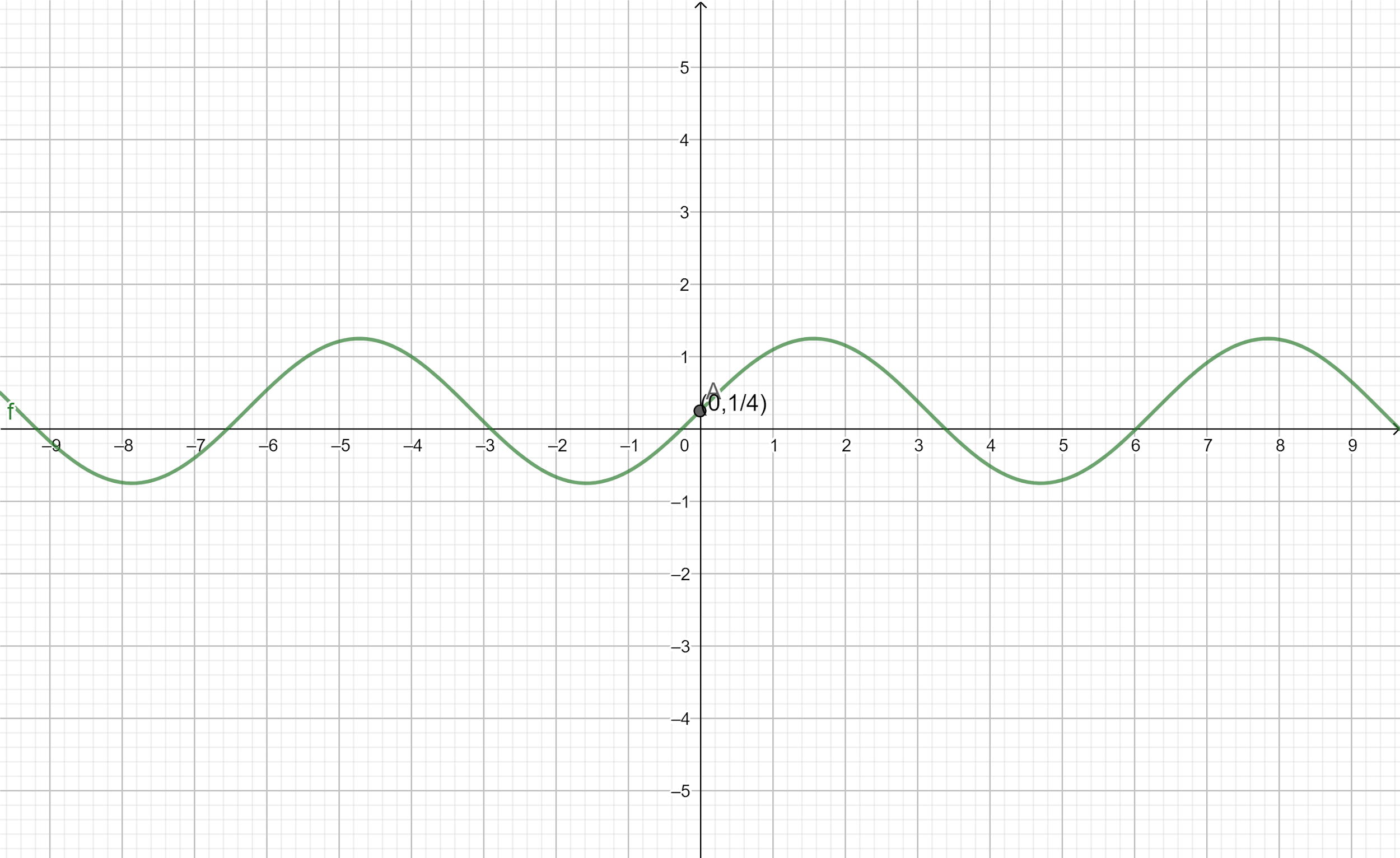
Step: 1 the normal $ \sin x $ graph makes a wave around the $ x - $ axis repeating itself every $ 2\pi $ .
To draw the graph of the function, make $ x - $ axis and $ y - $ axis with origin (0,0).
Plot the graph of $ \sin x $ function on the graph with $ x - $ axis.
Shift the graph of $ \sin x $ function by $ \dfrac{1}{4} $ towards up on the $ y - $ axis.
Adding $ \dfrac{1}{4} $ to every point we will find the graph of the function oscillating around the line passing through $ y = \dfrac{1}{4} $ .

Note:
Always try to remember the basic properties of $ \sin $ function. Find the period, rang, and domain of the $ \sin $ function. Start plotting the graph from origin. Check either the function is increasing or decreasing .Student must know the property of symmetric function, shift the graph of $ \sin x $ up by $ \dfrac{1}{4} $ unit passing through the line $ y = \dfrac{1}{4} $ .