
How do you graph \[y = \dfrac{1}{2}{x^2}?\]
Answer
555k+ views
Hint:The given question describes the operation of using arithmetic operations like addition/ subtraction/ multiplication/ division. Also, this problem involves substituting the \[x\] in the given equation to find the value of \[y\]. Because \[y\] is the function of \[x\] . By using the values of \[x\]and\[y\] we can easily draw the graph for the given equation.
Complete step by step solution:
The given equation is shown below,
\[y = \dfrac{1}{2}{x^2}\]
We would draw the graph for the above equation.
As a first step,
We would assume \[x\] value as given below,
\[x = ..... - 2, - 1,0,1,2,....\]
By substituting the above-mentioned \[x\] values in the given equation we can find the \[y\] values.
The given equation is,
\[y = \dfrac{1}{2}{x^2}\]\[ \to \left( 1 \right)\]
Let’s substitute \[x = - 2\] in the equation\[\left( 1 \right)\]we get,
\[y = \dfrac{1}{2}{x^2}\]
\[y = \dfrac{1}{2}{\left( { - 2} \right)^2}\]
\[
y = \dfrac{1}{2} \times 4 \\
y = 2 \\
\]
So, we get
When \[x = - 2\] the value of\[y\]is\[2\].
Let’s substitute\[x = - 1\] in the equation\[\left( 1 \right)\]we get,
\[y = \dfrac{1}{2}{x^2}\]
\[y = \dfrac{1}{2}{\left( { - 1} \right)^2}\]
\[
y = \dfrac{1}{2} \times 1 \\
y = \dfrac{1}{2} \\
\]
So we get,
When \[x = - 1\] the value of\[y\]is\[\dfrac{1}{2}\].
Let’s substitute \[x = 0\] in the equation \[\left( 1 \right)\], we get
\[y = \dfrac{1}{2}{x^2}\]
\[y = \dfrac{1}{2}{\left( 0 \right)^2}\]
\[y = 0\]
So we get,
When \[x = 0\] the value \[y\] is equal to\[0\].
Let’s substitute \[x = 1\] in the equation \[\left( 1 \right)\], we get
\[y = \dfrac{1}{2}{x^2}\]
\[y = \dfrac{1}{2}{\left( 1 \right)^2}\]
\[y = \dfrac{1}{2}\]
So we get,
When \[x = 1\] the value \[y\]is equal to \[\dfrac{1}{2}\].
Let’s substitute \[x = 2\] in the equation \[\left( 1 \right)\] we get,
\[y = \dfrac{1}{2}{x^2}\]
\[y = \dfrac{1}{2}{\left( 2 \right)^2}\]
\[
y = \dfrac{1}{2} \times 4 \\
y = 2 \\
\]
So we get,
When \[x = 2\] the value of\[y\]is\[2\].
Let’s make a tabular column by using the values of \[x\] and \[y\].
By using this table we can easily draw the graph for the given equation.
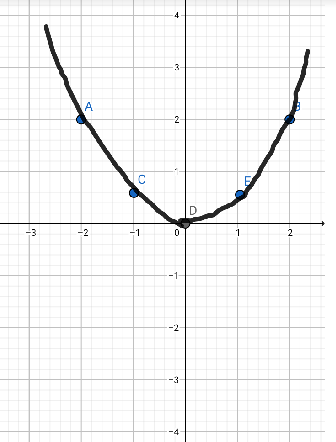
The above graph represents the equation \[y = \dfrac{1}{2}{x^2}\].
Note: This question describes the operation of addition/ subtraction/ multiplication/ division. Note that when the given equation is in the form of \[y = a{x^2}\] then the graph must be in parabolic shape.
Also, note that anything power zero will be one, and zero power anything will be one. When multiplying two different sign terms remember the following things,
1) \[\left( - \right) \times \left( - \right) = \left( + \right)\]
2) \[\left( + \right) \times \left( + \right) = \left( + \right)\]
3) \[\left( - \right) \times \left( + \right) = \left( - \right)\]
Complete step by step solution:
The given equation is shown below,
\[y = \dfrac{1}{2}{x^2}\]
We would draw the graph for the above equation.
As a first step,
We would assume \[x\] value as given below,
\[x = ..... - 2, - 1,0,1,2,....\]
By substituting the above-mentioned \[x\] values in the given equation we can find the \[y\] values.
The given equation is,
\[y = \dfrac{1}{2}{x^2}\]\[ \to \left( 1 \right)\]
Let’s substitute \[x = - 2\] in the equation\[\left( 1 \right)\]we get,
\[y = \dfrac{1}{2}{x^2}\]
\[y = \dfrac{1}{2}{\left( { - 2} \right)^2}\]
\[
y = \dfrac{1}{2} \times 4 \\
y = 2 \\
\]
So, we get
When \[x = - 2\] the value of\[y\]is\[2\].
Let’s substitute\[x = - 1\] in the equation\[\left( 1 \right)\]we get,
\[y = \dfrac{1}{2}{x^2}\]
\[y = \dfrac{1}{2}{\left( { - 1} \right)^2}\]
\[
y = \dfrac{1}{2} \times 1 \\
y = \dfrac{1}{2} \\
\]
So we get,
When \[x = - 1\] the value of\[y\]is\[\dfrac{1}{2}\].
Let’s substitute \[x = 0\] in the equation \[\left( 1 \right)\], we get
\[y = \dfrac{1}{2}{x^2}\]
\[y = \dfrac{1}{2}{\left( 0 \right)^2}\]
\[y = 0\]
So we get,
When \[x = 0\] the value \[y\] is equal to\[0\].
Let’s substitute \[x = 1\] in the equation \[\left( 1 \right)\], we get
\[y = \dfrac{1}{2}{x^2}\]
\[y = \dfrac{1}{2}{\left( 1 \right)^2}\]
\[y = \dfrac{1}{2}\]
So we get,
When \[x = 1\] the value \[y\]is equal to \[\dfrac{1}{2}\].
Let’s substitute \[x = 2\] in the equation \[\left( 1 \right)\] we get,
\[y = \dfrac{1}{2}{x^2}\]
\[y = \dfrac{1}{2}{\left( 2 \right)^2}\]
\[
y = \dfrac{1}{2} \times 4 \\
y = 2 \\
\]
So we get,
When \[x = 2\] the value of\[y\]is\[2\].
| \[x\] | \[ - 2\] | \[ - 1\] | \[0\] | \[1\] | \[2\] |
| \[y\] | \[2\] | \[\dfrac{1}{2}\] | \[0\] | \[\dfrac{1}{2}\] | \[2\] |
Let’s make a tabular column by using the values of \[x\] and \[y\].
By using this table we can easily draw the graph for the given equation.

The above graph represents the equation \[y = \dfrac{1}{2}{x^2}\].
Note: This question describes the operation of addition/ subtraction/ multiplication/ division. Note that when the given equation is in the form of \[y = a{x^2}\] then the graph must be in parabolic shape.
Also, note that anything power zero will be one, and zero power anything will be one. When multiplying two different sign terms remember the following things,
1) \[\left( - \right) \times \left( - \right) = \left( + \right)\]
2) \[\left( + \right) \times \left( + \right) = \left( + \right)\]
3) \[\left( - \right) \times \left( + \right) = \left( - \right)\]
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




