
How do you graph \[y = \dfrac{1}{2}x + 4\]?
Answer
556.8k+ views
Hint: Here we will plot the graph of the given equation by using the Intercept form. First, we will compare the given equation with the standard intercept form to get the value of the slope and \[y\]-intercept. We will substitute different values of \[x\] or \[y\] in the equation to get corresponding values of \[y\] or \[x\]. From this we will get coordinate points and using these points we will draw the required graph.
Complete step by step solution:
The equation of line is given as,
\[y = \dfrac{1}{2}x + 4\]……\[\left( 1 \right)\]
Comparing the equation with the intercept form \[y = mx + b\], we get
\[\begin{array}{l}m = \dfrac{1}{2}\\b = 4\end{array}\]
Now we will substitute different values of \[x\] in the given equation to find various coordinate points.
Substituting \[x = 0\] in equation, we get
\[y = \dfrac{1}{2} \times 0 + 4\]
Multiplying the terms, we get
\[ \Rightarrow y = 4\]
So, one of the coordinate points is \[\left( {0,4} \right)\].
Next, let \[y = 0\] be another point substituting it in equation \[\left( 1 \right)\], we get
\[\begin{array}{l}0 = \dfrac{1}{2}x + 4\\ \Rightarrow \dfrac{1}{2}x = - 4\end{array}\]
Multiplying both sides by 2, we get
\[ \Rightarrow x = - 8\]
So our second coordinate is \[\left( { - 8,0} \right)\]
Now, we will plot the two points in the graph and join them straight.
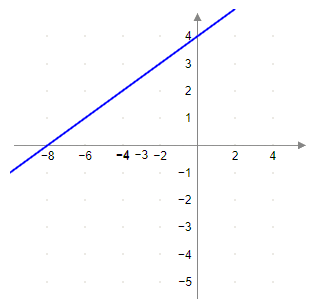
The graph of equation \[y = \dfrac{1}{2}x + 4\] is plotted as above.
Note:
A-Line is a one-dimensional figure that extends endlessly in both directions. It is also described as the shortest distance between any two points. There are many ways to draw the graph of the equation such as Point-slope Form, Intercept Form, Determinant Form, and many others. The Form we are using depends on the data we have. The scale can change as per the requirement so that the graph is plotted easily.
Complete step by step solution:
The equation of line is given as,
\[y = \dfrac{1}{2}x + 4\]……\[\left( 1 \right)\]
Comparing the equation with the intercept form \[y = mx + b\], we get
\[\begin{array}{l}m = \dfrac{1}{2}\\b = 4\end{array}\]
Now we will substitute different values of \[x\] in the given equation to find various coordinate points.
Substituting \[x = 0\] in equation, we get
\[y = \dfrac{1}{2} \times 0 + 4\]
Multiplying the terms, we get
\[ \Rightarrow y = 4\]
So, one of the coordinate points is \[\left( {0,4} \right)\].
Next, let \[y = 0\] be another point substituting it in equation \[\left( 1 \right)\], we get
\[\begin{array}{l}0 = \dfrac{1}{2}x + 4\\ \Rightarrow \dfrac{1}{2}x = - 4\end{array}\]
Multiplying both sides by 2, we get
\[ \Rightarrow x = - 8\]
So our second coordinate is \[\left( { - 8,0} \right)\]
Now, we will plot the two points in the graph and join them straight.
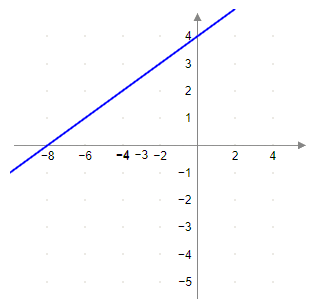
The graph of equation \[y = \dfrac{1}{2}x + 4\] is plotted as above.
Note:
A-Line is a one-dimensional figure that extends endlessly in both directions. It is also described as the shortest distance between any two points. There are many ways to draw the graph of the equation such as Point-slope Form, Intercept Form, Determinant Form, and many others. The Form we are using depends on the data we have. The scale can change as per the requirement so that the graph is plotted easily.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




