
How do you graph $y = \dfrac{{ - 1}}{4}x$ ?
Answer
546k+ views
Hint: In this question we asked to find the graph of the given function, we will do this by plotting the points, for this we will give some values for $x$ like 0, 1, 2, 3,…… simultaneously we will get the respective values for $y$, so after getting the values for $x$ and $y$ write the coordinates of the given equation in the form $\left( {x,y} \right)$, then plotting the coordinates on the graph we will get the required graph.
Complete step by step solution:
Given function is $y = \dfrac{{ - 1}}{4}x$, this is in the form of a linear equation with two variables.
Now take some values for $x$, as $x = - 8$,
$ \Rightarrow y = \dfrac{{ - 1}}{4}x$,
Now substitute $x = - 8$ in the above equation we get,
$ \Rightarrow $$y = \dfrac{{ - 1}}{4}\left( { - 8} \right)$,
Now simplifying we get,
$ \Rightarrow y = 2$,
Now take $x = - 4$,
$ \Rightarrow y = \dfrac{{ - 1}}{4}x$,
Now substitute $x = - 4$ in the above equation we get
$ \Rightarrow $$ \Rightarrow y = \dfrac{{ - 1}}{4}\left( { - 4} \right)$,
Now simplifying we get,
$ \Rightarrow y = 1$,
Now take $x = - 2$,
$ \Rightarrow y = \dfrac{{ - 1}}{4}x$,
Now substitute $x = - 2$in the above equation we get
$ \Rightarrow y = \dfrac{{ - 1}}{4}\left( { - 2} \right)$,
Now simplifying we get,
$ \Rightarrow y = \dfrac{1}{2}$,
Now take $x = 0$,
$ \Rightarrow y = \dfrac{{ - 1}}{4}x$,
Now substitute $x = 0$ in the above equation we get
$ \Rightarrow y = \dfrac{{ - 1}}{4}\left( 0 \right)$,
Now simplifying we get,
$ \Rightarrow y = 0$,
Now take $x = 2$,
$ \Rightarrow y = - \dfrac{1}{4}x$,
Now substitute $x = 2$in the above equation we get
$ \Rightarrow $$ \Rightarrow y = - \dfrac{1}{4}\left( 2 \right)$,
Now simplifying we get,
$ \Rightarrow y = - \dfrac{1}{2}$,
Now take $x = 4$,
$ \Rightarrow y = \dfrac{{ - 1}}{4}x$,
Now substitute $x = 4$in the above equation we get
$ \Rightarrow y = \dfrac{{ - 1}}{4}\left( 4 \right)$,
Now simplifying we get,
$ \Rightarrow y = - 1$,
Now take $x = 8$,
$ \Rightarrow y = \dfrac{{ - 1}}{4}x$,
Now substitute $x = 8$in the above equation we get
$ \Rightarrow y = \dfrac{{ - 1}}{4}\left( 8 \right)$,
Now simplifying we get,
$ \Rightarrow y = - 2$,
Now tabulating the values we get,
Now tabulate the values on the graph we get,
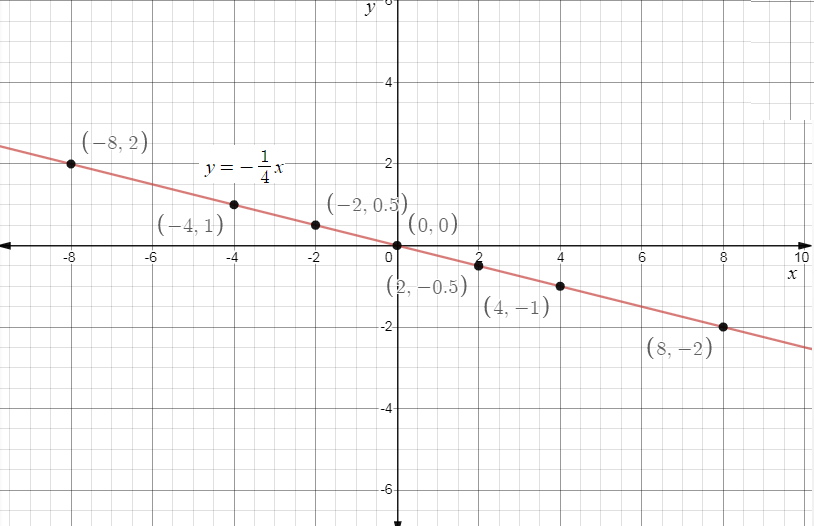
Final Answer:
$\therefore $The graph of the given function $y = \dfrac{{ - 1}}{4}x$ will be equal to,
Note:
We can represent every linear equation in two variables in a graph as a straight line in a coordinate plane. Points on the lines are known as the solution of the equation. So, the equation with one degree is known as linear equation. The expression of linear equations in a graph is known as graphing of linear equations in two variables.
Complete step by step solution:
Given function is $y = \dfrac{{ - 1}}{4}x$, this is in the form of a linear equation with two variables.
Now take some values for $x$, as $x = - 8$,
$ \Rightarrow y = \dfrac{{ - 1}}{4}x$,
Now substitute $x = - 8$ in the above equation we get,
$ \Rightarrow $$y = \dfrac{{ - 1}}{4}\left( { - 8} \right)$,
Now simplifying we get,
$ \Rightarrow y = 2$,
Now take $x = - 4$,
$ \Rightarrow y = \dfrac{{ - 1}}{4}x$,
Now substitute $x = - 4$ in the above equation we get
$ \Rightarrow $$ \Rightarrow y = \dfrac{{ - 1}}{4}\left( { - 4} \right)$,
Now simplifying we get,
$ \Rightarrow y = 1$,
Now take $x = - 2$,
$ \Rightarrow y = \dfrac{{ - 1}}{4}x$,
Now substitute $x = - 2$in the above equation we get
$ \Rightarrow y = \dfrac{{ - 1}}{4}\left( { - 2} \right)$,
Now simplifying we get,
$ \Rightarrow y = \dfrac{1}{2}$,
Now take $x = 0$,
$ \Rightarrow y = \dfrac{{ - 1}}{4}x$,
Now substitute $x = 0$ in the above equation we get
$ \Rightarrow y = \dfrac{{ - 1}}{4}\left( 0 \right)$,
Now simplifying we get,
$ \Rightarrow y = 0$,
Now take $x = 2$,
$ \Rightarrow y = - \dfrac{1}{4}x$,
Now substitute $x = 2$in the above equation we get
$ \Rightarrow $$ \Rightarrow y = - \dfrac{1}{4}\left( 2 \right)$,
Now simplifying we get,
$ \Rightarrow y = - \dfrac{1}{2}$,
Now take $x = 4$,
$ \Rightarrow y = \dfrac{{ - 1}}{4}x$,
Now substitute $x = 4$in the above equation we get
$ \Rightarrow y = \dfrac{{ - 1}}{4}\left( 4 \right)$,
Now simplifying we get,
$ \Rightarrow y = - 1$,
Now take $x = 8$,
$ \Rightarrow y = \dfrac{{ - 1}}{4}x$,
Now substitute $x = 8$in the above equation we get
$ \Rightarrow y = \dfrac{{ - 1}}{4}\left( 8 \right)$,
Now simplifying we get,
$ \Rightarrow y = - 2$,
Now tabulating the values we get,
| $x$ | $y$ |
| -8 | 2 |
| -4 | 1 |
| -2 | $\dfrac{1}{2}$ |
| 0 | 0 |
| 2 | $ - \dfrac{1}{2}$ |
| 4 | -1 |
| 8 | -2 |
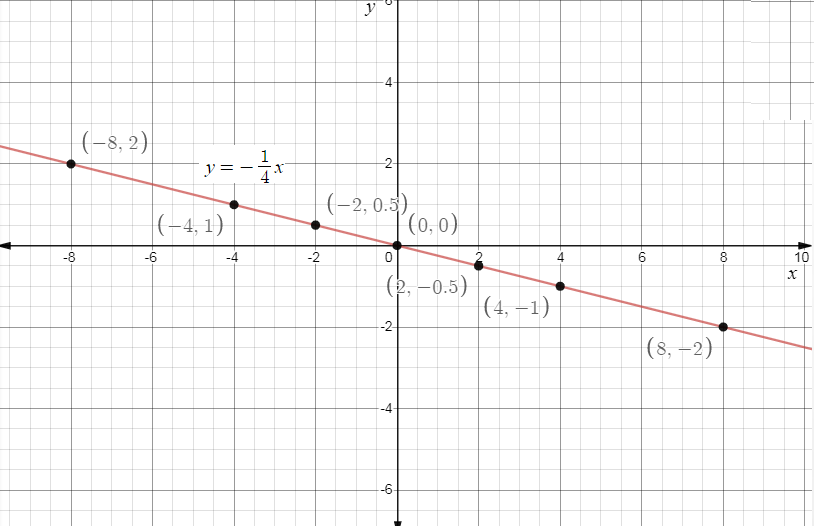
Now tabulate the values on the graph we get,

Final Answer:
$\therefore $The graph of the given function $y = \dfrac{{ - 1}}{4}x$ will be equal to,

Note:
We can represent every linear equation in two variables in a graph as a straight line in a coordinate plane. Points on the lines are known as the solution of the equation. So, the equation with one degree is known as linear equation. The expression of linear equations in a graph is known as graphing of linear equations in two variables.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




