
How do you graph $ y = {3^{ - x}} $ ?
Answer
530.4k+ views
Hint: In order to draw the graph of the given equation make a table of values for $ x $ and $ y $ in which put the values of $ x $ , then put the respective value of $ x $ in $ y $ , we get a point which is $ \left( {x,y} \right) $ . Follow these steps for at least five times. Then mark the points on the graph and join them and the graph of the equation is obtained.
Complete step by step solution:
We are given the equation $ y = {3^{ - x}} $ . To draw the graph of the equation, make a table of values for $ x $ and $ y $ by putting some random values in $ x $ and getting $ y $ with respect to that.
Let’s check for the table:
When we take $ x = - 3 $ we get $ y = {3^{ - \left( { - 3} \right)}} = {3^3} = 27 $ .
The first point we get is $ \left( { - 3,27} \right) $ .
Similarly let’s check for other six, seven points.
Taking $ x = - 2 $ we get $ y = {3^{ - \left( { - 2} \right)}} = {3^2} = 9 $
The second point we get is $ \left( { - 2,9} \right) $ .
Taking $ x = - 1 $ we get $ y = {3^{ - \left( { - 1} \right)}} = {3^1} = 3 $
The third point we get is $ \left( { - 1,3} \right) $ .
Taking $ x = 0 $ we get $ y = {3^0} = 1 $
The fourth point we get is $ \left( {0,1} \right) $ .
Taking $ x = 1 $ we get $ y = {3^{ - \left( 1 \right)}} = {3^{ - 1}} = \dfrac{1}{3} $
The fifth point we get is $ \left( {1,\dfrac{1}{3}} \right) $ .
Taking $ x = 2 $ we get $ y = {3^{ - \left( 2 \right)}} = {3^{ - 2}} = \dfrac{1}{9} $
The six points we get is $ \left( {2,\dfrac{1}{9}} \right) $ .
We can go for some other points or we can stop here only.
The table obtained is:
Now, put the points in the graph and join the and we get the graph for the equation $ y = {3^{ - x}} $ :
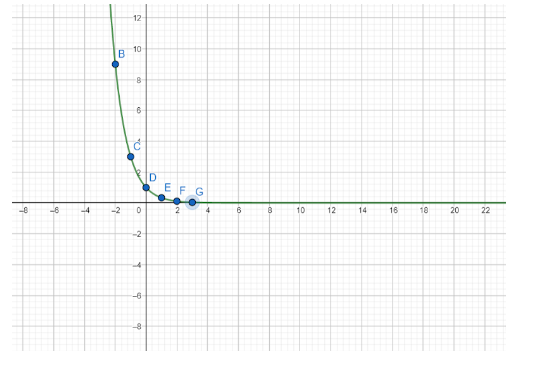
Note: Always make a table of relation of variables for this type of graph which would help to write points and then mark on the graph.
Always cross check the graph once, their points are according to the equation or not.
There can be an error in calculating $ y $ from $ x $ .
Complete step by step solution:
We are given the equation $ y = {3^{ - x}} $ . To draw the graph of the equation, make a table of values for $ x $ and $ y $ by putting some random values in $ x $ and getting $ y $ with respect to that.
Let’s check for the table:
When we take $ x = - 3 $ we get $ y = {3^{ - \left( { - 3} \right)}} = {3^3} = 27 $ .
The first point we get is $ \left( { - 3,27} \right) $ .
Similarly let’s check for other six, seven points.
Taking $ x = - 2 $ we get $ y = {3^{ - \left( { - 2} \right)}} = {3^2} = 9 $
The second point we get is $ \left( { - 2,9} \right) $ .
Taking $ x = - 1 $ we get $ y = {3^{ - \left( { - 1} \right)}} = {3^1} = 3 $
The third point we get is $ \left( { - 1,3} \right) $ .
Taking $ x = 0 $ we get $ y = {3^0} = 1 $
The fourth point we get is $ \left( {0,1} \right) $ .
Taking $ x = 1 $ we get $ y = {3^{ - \left( 1 \right)}} = {3^{ - 1}} = \dfrac{1}{3} $
The fifth point we get is $ \left( {1,\dfrac{1}{3}} \right) $ .
Taking $ x = 2 $ we get $ y = {3^{ - \left( 2 \right)}} = {3^{ - 2}} = \dfrac{1}{9} $
The six points we get is $ \left( {2,\dfrac{1}{9}} \right) $ .
We can go for some other points or we can stop here only.
The table obtained is:
| X | Y |
| -3 | 27 |
| -2 | 9 |
| -1 | 3 |
| 0 | 1 |
| 1 | 0.33 |
| 2 | 0.11 |
| 3 | 0.04 |
Now, put the points in the graph and join the and we get the graph for the equation $ y = {3^{ - x}} $ :

Note: Always make a table of relation of variables for this type of graph which would help to write points and then mark on the graph.
Always cross check the graph once, their points are according to the equation or not.
There can be an error in calculating $ y $ from $ x $ .
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

A moving boat is observed from the top of a 150 m high class 10 maths CBSE




