Question

How do you graph ${{x}^{3}}+3{{x}^{2}}-6x$ ? \[\]

Answer 1

Hint: We denote the given cubic polynomial as $f\left( x \right)={{x}^{3}}+3{{x}^{2}}-6x$. We find the zeros of the polynomial $f\left( x \right)$ using linear factorization and quadratic formula $x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}$ to find where curve of $f\left( x \right)$ cuts $x-$axis. If $x=p,q,r$ are the roots then we find if there exists a minima or maxima within intervals $\left( p,q \right),\left( q,r \right)$ using a second derivative test. We join the extrema points and join them as a smooth curve. \[\]

Complete step by step solution:
Let us denote the given cubic polynomial as $f\left( x \right)$ to have;
\[f\left( x \right)={{x}^{3}}+3{{x}^{2}}-6x\]
Let us find the zeros of the above polynomial $f\left( x \right)$ to find a at which point the curve of $f\left( x \right)$ cuts $x-$axis where $f\left( x \right)=0$. So we take $x$ common from the polynomial and equate it to zero to have;
\[\begin{align}
  & f\left( x \right)=0 \\
 & \Rightarrow x\left( {{x}^{2}}+3x-6 \right)=0 \\
\end{align}\]
So we have one zero of the polynomial is $x=0$. We find the other two zeros as the root of quadratic equation ${{x}^{2}}+3x-6=0$ by quadratic formula to have;
\[\begin{align}
  & x=\dfrac{-3\pm \sqrt{{{3}^{2}}-4\cdot 1\left( -6 \right)}}{2\cdot 1} \\
 & \Rightarrow x=\dfrac{-3\pm \sqrt{9+24}}{2} \\
 & \Rightarrow x=\dfrac{-3+\sqrt{33}}{2},\dfrac{-3-\sqrt{33}}{2} \\
 & \Rightarrow x\approx \dfrac{-3+5.74}{2},\dfrac{-3-5.74}{2} \\
\end{align}\]
So the roots are
\[\Rightarrow x\approx 1.37,-4.37\]
So the curve will cut the $x-$axis and the change it sign at $x=-4.37,x=0,x=1.37$. Now we use a second derivative test to find the maxima or minima in the intervals $\left( -4.37,0 \right),\left( 0,1.37 \right)$. We have the first derivative as ;
\[\begin{align}
  & {{f}^{'}}\left( x \right)=\dfrac{d}{dx}\left( {{x}^{3}}+3{{x}^{2}}-6x \right) \\
 & \Rightarrow {{f}^{'}}\left( x \right)=3{{x}^{2}}+6x-6 \\
\end{align}\]
Let us find the second derivative to have;
\[\Rightarrow {{f}^{''}}\left( x \right)=6x+6\]
Now we equate the first derivative to 0 to find the critical points from ${{f}^{'}}\left( x \right)=0$. ;
\[\begin{align}
  & {{f}^{'}}\left( x \right)=0 \\
 & \Rightarrow 3{{x}^{2}}+6x-6=0 \\
 & \Rightarrow {{x}^{2}}+2x-2=0 \\
\end{align}\]
We use the quadratic formula again to have;
\[\begin{align}
  & \Rightarrow x=\dfrac{-2\pm \sqrt{{{2}^{2}}-4\cdot 1\cdot \left( -2 \right)}}{2\cdot 1} \\
 & \Rightarrow x=\dfrac{-2\pm \sqrt{{{2}^{2}}+8}}{2\cdot 1} \\
 & \Rightarrow x=\dfrac{-2+\sqrt{12}}{2},\dfrac{-2-\sqrt{12}}{2} \\
 & \Rightarrow x\approx 0.73,-2.73 \\
\end{align}\]
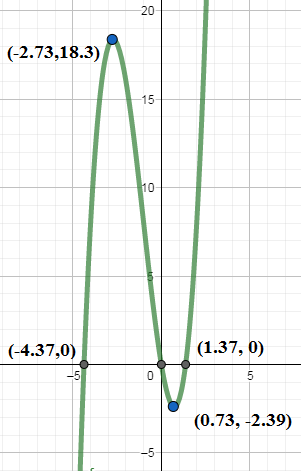
Since we have ${{f}^{''}}\left( 1.41 \right)=6\left( 1.41 \right)+6 > 0$ we get a minima at $x=1.41$ and the minimum value is $f\left( 1.41 \right)=-2.39$. Since we have ${{f}^{''}}\left( -2.73 \right)=6\left( -2.73 \right)+6 < 0$ we get maxima at $x=-2.73$ and the maximum value is $f\left( -2.73 \right)=18.39$. We also see that at left of $x=-4.37$ as $x\to -\infty $ and at the right of $x=1.37$ as $x\to \infty $ we have $f\left( x \right)\to \infty $. So we draw the rough graph as.\[\]

Note: We note that a critical points of the function $f\left( x \right)$ are those points where ${{f}^{'}}\left( x \right)$ is not defined or ${{f}^{'}}\left( x \right)=0$. The first derivative polynomial function is defined everywhere. The second derivative test tell us that we get a minima at critical point $x=c$ if ${{f}^{'}}\left( c \right) < 0 $ and a maxima if ${{f}^{'}}\left( c \right) > 0$. If ${{f}^{'}}\left( c \right)=0$ the second derivative test fails. We can also use the first derivative test where we observe the change of sign of ${{f}^{'}}\left( x \right)$ at $x=c$.