Question

How do you graph \[{{x}^{2}}-14x+{{y}^{2}}-14y+89=0\]?

Answer 1

Hint: In this problem, we have to graph the given equation of the circle. Here we have to convert the given equation in the form of the general equation of the circle to find the centre and the radius, which we can plot in the graph. We can first take the constant term to the right-hand side, we can then add the term on the left-hand side, which will become an expansion of the algebraic whole square formula, we can then convert the given equation into its standard form to draw the graph.

Complete step-by-step answer:
We know that the given equation of the circle is,
\[{{x}^{2}}-14x+{{y}^{2}}-14y+89=0\]
We know that the general equation of the circle is,
\[{{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}\]
Where \[\left( a,b \right)\] is the centre and r is the radius.
Here we have to convert the given equation in the form of the general equation of the circle to find the centre and the radius, which we can plot in the graph.
We can now write the above equation as,
 \[\Rightarrow {{x}^{2}}-14x+{{y}^{2}}-14y=-89\]
We can now add 49 on both sides we get
\[\Rightarrow {{x}^{2}}-14x+49+{{y}^{2}}-14y=-89+49\]
We can see that the above first three terms is an expansion of the whole square formula, which can also be written as,
\[\Rightarrow {{\left( x-7 \right)}^{2}}+{{y}^{2}}-14y=-40\]
We can again add 49 on both sides for the y term to be converted, we get
\[\Rightarrow {{\left( x-7 \right)}^{2}}+{{y}^{2}}-14y+49=-40+49\]
We can now write the above step as,
\[\Rightarrow {{\left( x-7 \right)}^{2}}+{{\left( y-7 \right)}^{2}}=9\]
We can see that the above step is in the form of the general equation of the circle, where \[\left( 7,7 \right)\] is the centre point and r = 3.
The graph of \[{{x}^{2}}-14x+{{y}^{2}}-14y+89=0\] is ,

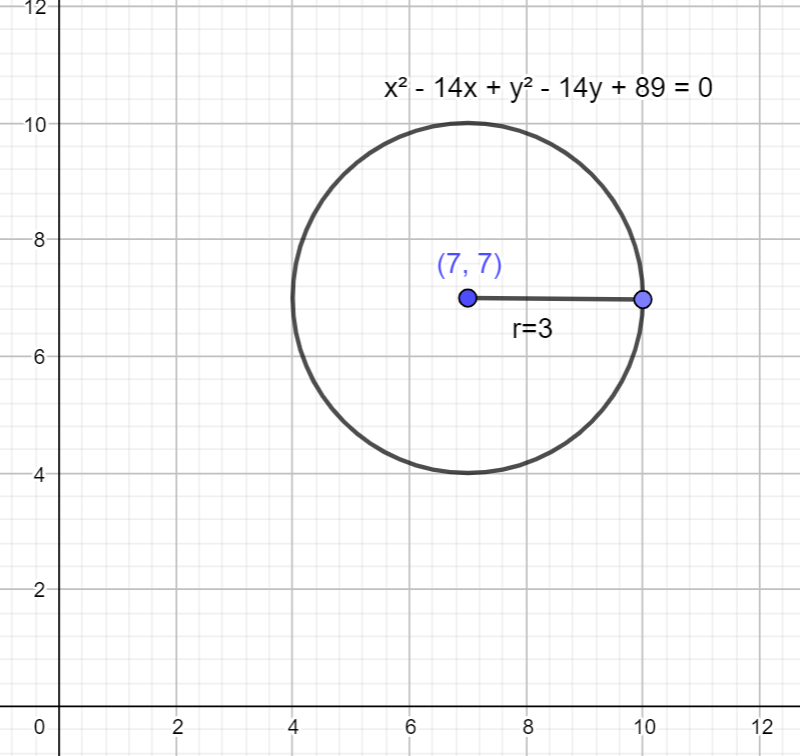
Note: Students make mistakes while adding the numbers which will expand the term into its whole square formula. We should always remember the general equation of the circle\[{{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}\] Where \[\left( a,b \right)\] is the centre and r is the radius.