Question

How do you graph \[{x^2} - 4y + 16 = 0\]?

Answer 1

Hint: To graph the given equation let us graph using intercepts, i.e., we need to find x and y intercepts. To find the x-intercept, set y = 0 and solve for x, to find the y-intercept, set x = 0 and solve for y, hence by solving we get the x and y intercepts and then graph the solution.

Complete step by step solution:
Let us write the given equation:
 \[{x^2} - 4y + 16 = 0\]
To graph the solution for the given equation, we need to find x and y intercepts.
Let us find the y-intercepts: To find the y-intercept, set \[x = 0\] in the given equation,
and solve for y as:
 \[{x^2} - 4y + 16 = 0\]
 \[ \Rightarrow {\left( 0 \right)^2} - 4y + 16 = 0\]
 \[ \Rightarrow - 4y + 16 = 0\]
As, we need the value of y, hence shift the terms as:
 \[ \Rightarrow - y = \dfrac{{ - 16}}{4}\]
Evaluating the terms, we get:
 \[ \Rightarrow - y = - 4\]
Hence, we get:
 \[ \Rightarrow y = 4\]
Thus y-intercept is \[\left( {0,4} \right)\].
Now, let us find the x-intercepts: To find the x-intercept, set \[y = 0\] in the given equation and solve for x i.e.,
 \[{x^2} - 4y + 16 = 0\]
 \[ \Rightarrow {x^2} - 4\left( 0 \right) + 16 = 0\]
 \[ \Rightarrow {x^2} + 16 = 0\]
Hence, the roots of this equation are imaginary; thus, the curve will not touch the x axis.
And therefore, this is quadratic equation which represents equation of parabola which is symmetrical about y axis and the Graph is shown as:

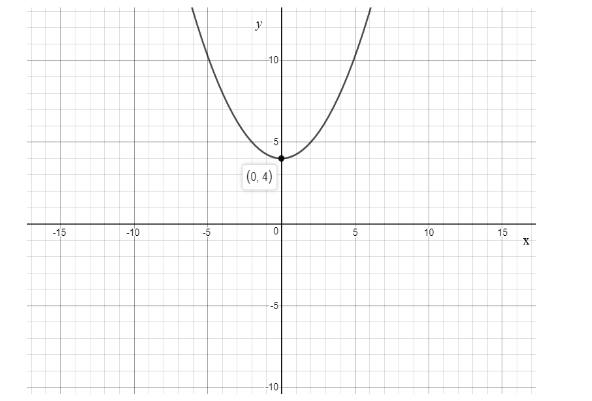
Note: The given method of finding x- and y-intercepts will be used throughout our algebraic equation, because it works for any equation. We can also use slope intercept form to graph the solution if they ask to find the slope for the given equation using the form \[y = mx + b\] and solve for x and y intercepts and any line can be graphed using two points i.e., select two x values, and plug them into the equation to find the corresponding y values.