Question

How do you graph ${{x}^{2}}+{{y}^{2}}+8x-6y+16=0$?

Answer 1

Hint: If you carefully look at the equation you can see that the above equation is the equation of a circle. Because we know that the equation of a circle is as follows: ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$. Now, to graph this circle, we need the centre of the circle and the radius of the circle. And we also know that centre of the circle from the equation of a circle i.e. $\left( -g,-f \right)$ and the radius of the circle is equal to $\sqrt{{{g}^{2}}+{{f}^{2}}-c}$.

Complete step by step answer:
In the above problem, we are asked to graph the following equation:
${{x}^{2}}+{{y}^{2}}+8x-6y+16=0$ ………….. (1)
The above equation is in the form of equation of circle and we know that the general form of equation of a circle is as follows:
${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ …………. (2)
The centre of the above circle is as follows:
$\left( -g,-f \right)$
Now, comparing the equation (1 & 2) we get,
$\begin{align}
  & \Rightarrow 2g=8 \\
 & \Rightarrow g=\dfrac{8}{2}=4; \\
 & 2f=-6 \\
 & \Rightarrow f=-\dfrac{6}{2}=-3 \\
\end{align}$
Now, substituting the above values of g and f in the centre we get,
$\begin{align}
  & \Rightarrow \left( -4,-\left( -3 \right) \right) \\
 & =\left( -4,3 \right) \\
\end{align}$
Hence, we got the centre of the given circle as (-4, 3).
Now, we are going to find the radius of the circle and we know that the formula for radius of the circle is equal to:
$=\sqrt{{{g}^{2}}+{{f}^{2}}-c}$
On comparing eq. (1 and 2) we will get the value of c as follows:
$c=16$
Now, substituting the values of g, f and c in the above formula of radius we get,
$\begin{align}
  & =\sqrt{{{\left( -4 \right)}^{2}}+{{\left( 3 \right)}^{2}}-16} \\
 & =\sqrt{16+9-16} \\
 & =\sqrt{9} \\
 & =3 \\
\end{align}$
Hence, we have calculated the value of centre and radius as (-4, 3) and 3 respectively.
Now, plotting the centre and radius on the graph and we get,

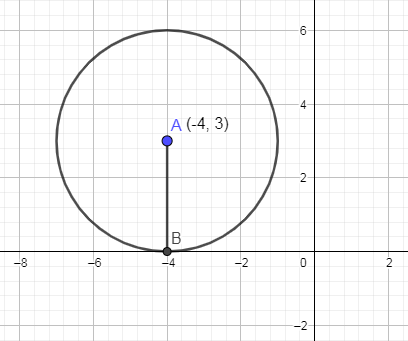
In the above graph, A is the centre of the circle and AB is the radius of the circle.
Hence, we have drawn the given equation on the graph.

Note: The mistake that could be possible in the above problem is that while writing the centre of the circle you must forget to put the negative sign in front of g and f. So, make sure after finding the value of g and f from the given equation always put the negative sign in front of g and f.
In the below, we have shown the negative signs in front of “g and f”.
(-g, -f)
So, don’t forget to put this negative sign in front of g and f.