Question

How do you graph \[f(x) = {x^2} - 4x + 5\] ?

Answer 1

Hint: In order graph the parabola to the above quadratic equation, first identify the nature of roots of the equation by finding the value of the determinant using the formula $D = {b^2} - 4ac,D > 0$ means the both the roots are distinct and real.
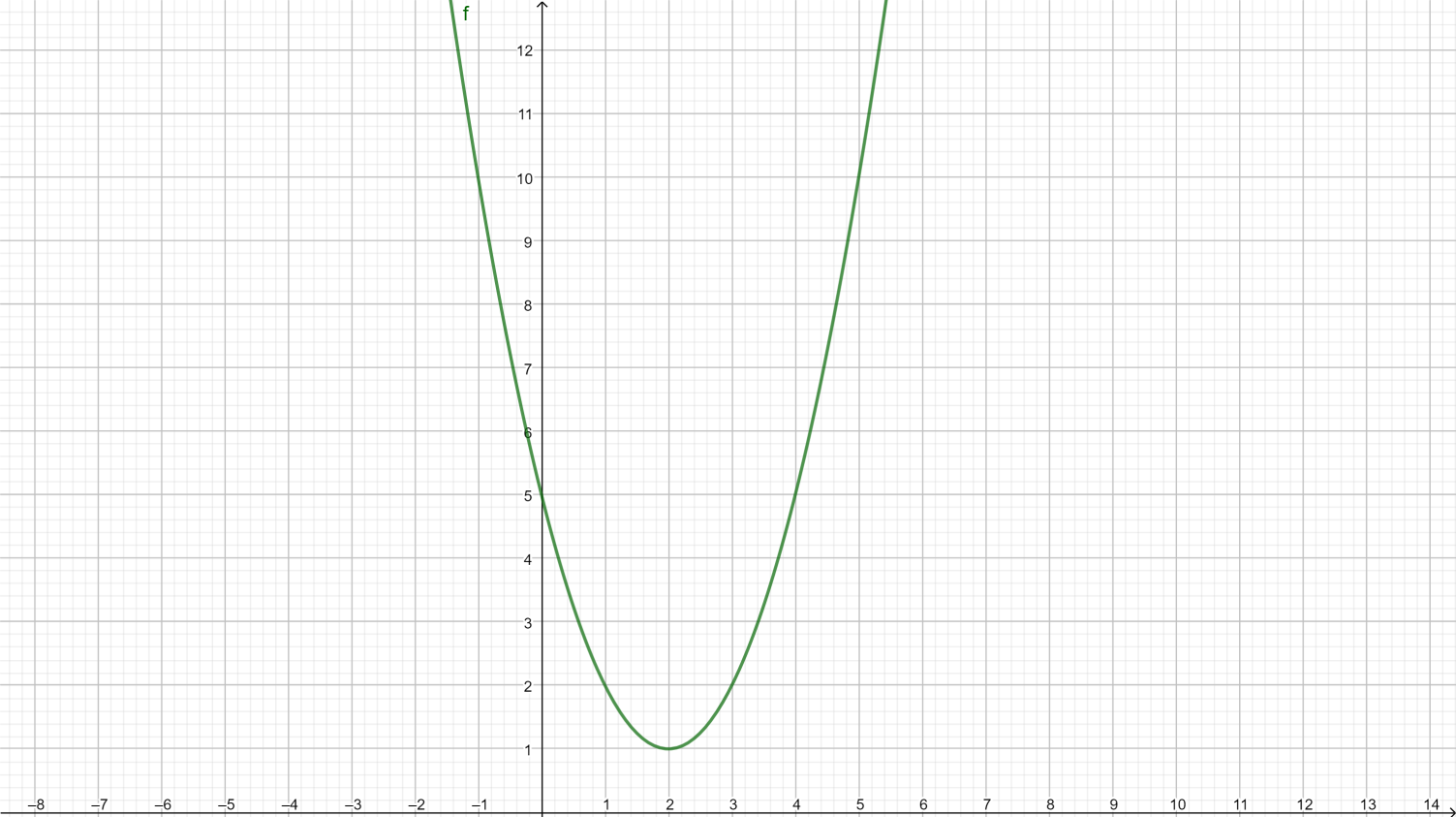
The given expression is a quadratic polynomial. The graph of the quadratic polynomial is a parabola, with the horns pointing upwards if \[a > 0\].

Complete step-by-step solution:
\[{x^2} - 4x + 5\] Is similar to \[a{x^2} + bx + c\]
It can be observed that \[a > 0\]
Therefore, it will be an upward opening parabola. Now we need to find the intercepts of the parabola.
For $y$-intercept, substituting \[x = 0\]
\[f(x) = {x^2} - 4x + 5\]
After substitution,
\[ \Rightarrow f(0) = {(0)^2} - 4(0) + 5\]
Now Simplified,
\[ \Rightarrow f(0) = 5\]
For x-intercept, substituting \[y = 0\]
\[ \Rightarrow {x^2} - 4x + 5 = 0\]
Roots of the above equation can be found by using the discriminant using the following formula
\[{x_{1,2}} = \dfrac{{\left( { - b \pm \sqrt {{b^2} - 4ac} } \right)}}{{2a}}\]
Substitute the values of the given
\[ \Rightarrow {x_{1,2}} = \dfrac{{\left( { - ( - 4) \pm \sqrt {{{( - 4)}^2} - 4(1)(5)} } \right)}}{{2(1)}}\]
On simplified,
\[ \Rightarrow {x_{1,2}} = \dfrac{{\left( {4 \pm \sqrt {16 - 20} } \right)}}{2}\]
By calculating,
${x_{1,2}} = \left( {\dfrac{{4 \pm 2i}}{2}} \right)$
\[ \Rightarrow \Delta < 0\]Therefore, no intercepts.
Now, to find the vertex, we follow the following steps-
$X - vertex{\text{ will be }}$
\[{x_v} = - \dfrac{b}{{2a}}\]
\[ \Rightarrow {x_v} = - \dfrac{{ - 4}}{2}\]
$\therefore {x_v} = 2$
$Y - vertex{\text{ will be}}$
\[{y_v} = - \dfrac{\Delta }{{4a}}\]
\[ \Rightarrow {y_v} = - \dfrac{{ - 4}}{4} = 1\]

Note: A quadratic equation
\[a{x^2} + bx + c\],
with the leading coefficient \[a \ne 0\], has two roots that may be real - equal or different - or complex. The roots can be found from the quadratic formula:
\[{x_{1,2}} = \dfrac{{\left( { - b \pm \sqrt {{b^2} - 4ac} } \right)}}{{2a}}\],

In addition to the four arithmetic operations, the formula includes a square root. The expression under the square root, \[D = {b^2} - 4ac\] - known as the discriminant - may be positive, zero, or negative. Correspondingly, the equation may have two real and distinct roots, two equal real roots, or two conjugate complex roots.
The applet allows one to experiment by changing the coefficients of the polynomial by dragging the three scrollbars at the top of the applet.)
(The maximum and minimum values on the axes can also be changed by clicking at the numbers at the endpoints - a little off their vertical mid-axis.)
The graph of the quadratic polynomial is a parabola, with the horns pointing upwards if \[a > 0\] or downwards if \[a < 0\].
Observe on the graph the behavior of the roots as you change the other two coefficients, b and c. If real, they lie on the x-axis symmetrically with respect to the vertical line through the parabola's extreme point. If complex, they simply lie on that line symmetrically with respect to the x-axis.