Question

How do you graph and solve $|2x+3|\le 15$?

Answer 1

Hint:
To graph an equation that involves an absolute value operator, we must first get rid of the absolute value equation by dividing the equation into different parts. Then graph the equations of these parts separately.

Complete step by step solution:
As the same suggests, inequality refers to something (say some variable) being not exactly equal to something. In other words, we can say that the value of the quantity is not exactly known but we do know some restriction or condition for the value of the quantity.
The given inequality says that $|2x+3|\le 15$.
Let us first solve this inequality.
We know that when $2x+3\ge 0$, $|2x+3|=2x+3$
This means that when $x\ge -\dfrac{3}{2}$, $|2x+3|=2x+3$
Now, we have to solve for the inequality $2x+3\le 15$ for $x\ge -\dfrac{3}{2}$
$\Rightarrow x\le \dfrac{15-3}{2}$
$\Rightarrow x\le 6$
This means that for $|2x+3|\le 15$ to be valid, $x\ge -\dfrac{3}{2}$ and $x\le 6$
i.e. $-\dfrac{3}{2}\le x\le 6$ ….. (i)
Next, we know that when $2x+3<0$, $|2x+3|=-(2x+3)=-2x-3$
This means that when $x<-\dfrac{3}{2}$, $|2x+3|=-2x-3$
Now, we have to solve for the inequality $-2x-3\le 15$ for $x<-\dfrac{3}{2}$
$\Rightarrow -x\le \dfrac{15+3}{2}$
$\Rightarrow -x\le 9$
$\Rightarrow x\ge -9$
This means that for $|2x+3|\le 15$ to be valid, $x<-\dfrac{3}{2}$ and $x\ge -9$
i.e. $-9\le x<\dfrac{-3}{2}$ …. (ii)
If we combine (i) and (ii), we get that the solution of the inequality is $-9\le x\le 6$
Now, the graph of the inequality will be a rectangular region bounded by the lines $x=-9$ and $x=6$.

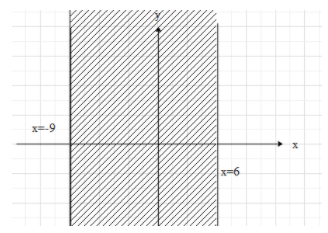
Note:
To plot the graph of the given inequality, $2x+3\le 15$ for $x\ge -\dfrac{3}{2}$.
We can do this by first plotting the line $2x+3=15$. The region towards the left of this will satisfy the inequality.
Then we can do the same procedure for $-2x-3\le 15$.
Plot the line $-2x-3=15$ and mark the region towards the right of this line.