Question

How do you graph \[{a_n} = 2{\left( 3 \right)^{n - 1}}\] ?

Answer 1

Hint: Here in this given equation given the nth term of geometric series when we give the n values we get the geometric series now give the values to the n like 0, 1, 2, 3, … simultaneously we get the values of \[{a_0}\] , \[{a_1}\] , \[{a_2}\] … Now we construct the coordinates of a given series i.e., (x,y) by using the coordinates to construct the graph. We assign the value of n values as x and the determined value \[{a_n}\] as y and we plot the graph.

Complete step-by-step answer:
Consider the equation \[{a_n} = 2{\left( 3 \right)^{n - 1}}\]
Which is a geometric sequence, The sequence cannot be represented by a continuous graph as \[{a_n}\] is only defined \[\forall n \in N\]
By giving the n values …-3,-2,-1, 0, 1, 2, 3, … simultaneously we get the values of \[{a_n}\]
Put n=-3
Then \[ \Rightarrow \,{a_{ - 3}} = 2{\left( 3 \right)^{ - 3 - 1}}\]
 \[ \Rightarrow \,\,\,{a_{ - 3}} = \dfrac{2}{{{3^4}}}\]
 \[\therefore \,\,\,{a_{ - 3}} = 0.02469\]
Therefore, co-ordinate \[\left( {x,y} \right) = \left( { - 3,0.02469} \right)\]
Put n=-2
 \[ \Rightarrow \,{a_{ - 2}} = 2{\left( 3 \right)^{ - 2 - 1}}\]
 \[ \Rightarrow \,\,\,{a_{ - 2}} = \dfrac{2}{{{3^3}}}\]
 \[\therefore \,\,\,{a_{ - 2}} = 0.07407\]
 Therefore, co-ordinate \[\left( {x,y} \right) = \left( { - 2,0.07407} \right)\]
Put n=-1
 \[ \Rightarrow \,{a_{ - 1}} = 2{\left( 3 \right)^{ - 1 - 1}}\]
 \[ \Rightarrow \,\,\,{a_{ - 1}} = \dfrac{2}{{{3^2}}}\]
 \[\therefore \,\,\,{a_{ - 1}} = 0.2222\]
 Therefore, co-ordinate \[\left( {x,y} \right) = \left( { - 1,0.2222} \right)\]
Put n=0
 \[ \Rightarrow \,{a_0} = 2{\left( 3 \right)^{0 - 1}}\]
 \[ \Rightarrow \,\,\,{a_0} = \dfrac{2}{3}\]
 \[\therefore \,\,\,{a_0} = 0.6666\]
 Therefore, co-ordinate \[\left( {x,y} \right) = \left( {0,0.6666} \right)\]
Put n=1
 \[ \Rightarrow \,{a_1} = 2{\left( 3 \right)^{1 - 1}}\]
 \[ \Rightarrow \,{a_1} = 2{\left( 3 \right)^0}\]
 \[\therefore \,\,\,{a_1} = 2\]
 Therefore, co-ordinate \[\left( {x,y} \right) = \left( {1,0} \right)\]
Put n=2
 \[ \Rightarrow \,{a_2} = 2{\left( 3 \right)^{2 - 1}}\]
 \[ \Rightarrow \,{a_2} = 2{\left( 3 \right)^1}\]
 \[\therefore \,\,\,{a_2} = 6\]
 Therefore, co-ordinate \[\left( {x,y} \right) = \left( {2,6} \right)\]
Put n=3
 \[ \Rightarrow \,{a_3} = 2{\left( 3 \right)^{3 - 1}}\]
 \[ \Rightarrow \,{a_3} = 2{\left( 3 \right)^2}\]
 \[\therefore \,\,\,{a_2} = 18\]
 Therefore, co-ordinate \[\left( {x,y} \right) = \left( {3,18} \right)\]
And so on
Now, the graph of the of the given geometric progression series \[{a_n} = 2{\left( 3 \right)^{n - 1}}\] is given by

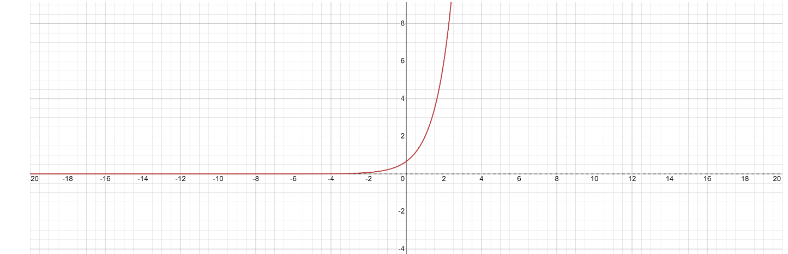
Note: First we simplify the given equation and we plot the graph for the points. The graph is plotted x-axis versus y axis. The graph is two dimensional. By the equation of a graph, we can plot the graph by assuming the value of x. we can’t assume the value of y. because the value of y depends on the value of x. Hence, we have plotted the graph.