Question

How do you graph $4x + 3y > - 12$?

Answer 1

Hint:
First, we have to convert given inequation and inequation. Next, put $y = 0$ in this equation to get the point where the line meets with $x$-axis. Similarly, put $x = 0$ to obtain a point where the line meets with $y$-axis. Next, join the points obtained to obtain the graph of the line obtained from the given inequation. Next, determine the region represented by the given inequality and consider the point $O\left( {0,0} \right)$. If the inequation is satisfied, then shade the portion of the plane which contains the chosen point; otherwise shade the portion which does not contain the chosen point. Finally, the shaded region obtained represents the desired solution set.

Formula used:
In order to find the solution set of a linear inequation in two variables, we follow the following algorithm.
Step I: Convert the given inequation, say $ax + by \leqslant c$, into the equation $ax + by = c$ which represents a straight line in $xy$-plane.
Step II Put $y = 0$ in the equation obtained in step I to get the point where the line meets with $x$-axis. Similarly, put $x = 0$ to obtain a point where the line meets with $y$-axis.
Step III Join the points obtained in step II to obtain the graph of the line obtained from the given inequation. In case of a strict inequality i.e., $ax + by > c$, draw the dotted line, otherwise mark it a thick line.
Step IV Choose a point, if possible $\left( {0,0} \right)$, not lying on this line: Substitute its coordinates in the inequation. If the inequation is satisfied, then shade the portion of the plane which contains the chosen point; otherwise shade the portion which does not contain the chosen point.
Step V The shaded region obtained in step IV represents the desired solution set.

Complete step by step solution:
First, we have to convert given inequation into inequation.
So, converting the given inequation we obtain $4x + 3y = - 12$.
Now, put $y = 0$ in the equation $4x + 3y = - 12$ to get the point where the line meets with $x$-axis.
\[ \Rightarrow 4x = - 12\]
Divide both side of the equation by $4$, we get
$ \Rightarrow x = - 3$
Now, put $x = 0$ in the equation $4x + 3y = - 12$ to get the point where the line meets with $y$-axis.
$ \Rightarrow 3y = - 12$
Divide both side of the equation by $3$, we get
$ \Rightarrow y = - 4$
So, this line meets the $x$-axis at $A\left( { - 3,0} \right)$ and $y$-axis at $B\left( {0, - 4} \right)$.
We plot these points and join them by a dotted line.

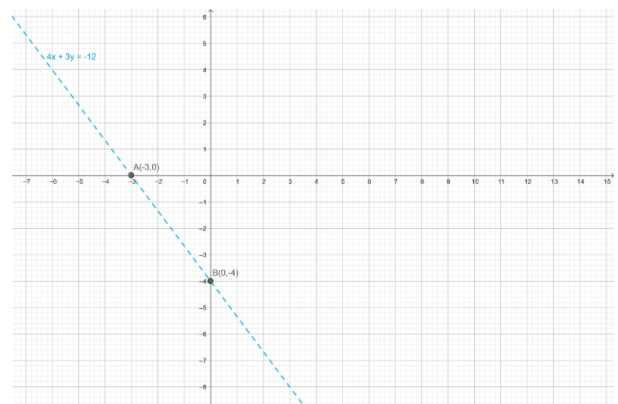
This line divides the $xy$-plane in two parts.
To determine the region represented by the given inequality consider the point $O\left( {0,0} \right)$.
Clearly $\left( {0,0} \right)$ satisfies the inequality as $0 > - 12$.
So, the region containing the origin is represented by the given inequation.

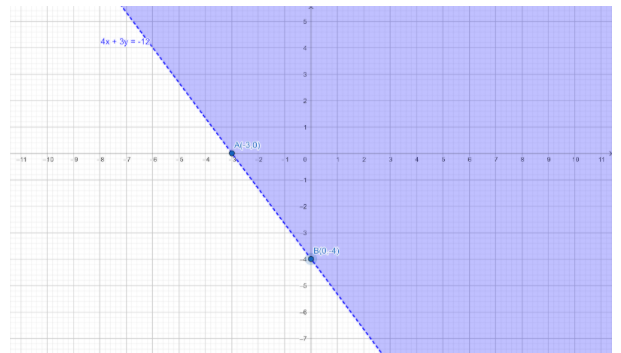
This region represents the solution set of the given inequation.

Note:
In case of the inequalities $ax + by \leqslant c$ and $ax + by \geqslant c$ points on the line are also a part of the shaded region while in case of inequalities $ax + by < c$ and $ax + by > c$ points on the line $ax + by = c$ are not in the shaded region.