Question

How do you graph \[4x + 3y - 12 = 0\]?

Answer 1

Hint: In this question we have to draw the linear equation given, for this we have to first find the intercepts we have to assume one variable as zero to find the value of other variable i.e., if we have to find \[x\]-intercept we have to put \[y = 0\], and if we have to find \[y\]-intercept we have to put \[x = 0\], and then plot the intercepts on the graph to get the required graph.

Complete step-by-step solution:
Now the given equation is \[4x + 3y - 12 = 0\],
First transform the equation in terms of \[y\], first take all terms except \[y\] to the right hand side then the equation becomes,
\[ \Rightarrow 3y = 12 - 4x\],
Now divide both sides by 3, we get,
\[ \Rightarrow \dfrac{{3y}}{3} = \dfrac{{12 - 4x}}{3}\],
Now simplifying we get,
\[ \Rightarrow y = \dfrac{{12}}{3} - \dfrac{{4x}}{3}\],
Now further simplification we get,
\[ \Rightarrow y = 4 - \dfrac{{4x}}{3}\],
Now we will assume \[x = 0\] to find the \[y\]-intercept, substituting the value of \[x\] in the equation we get,
\[ \Rightarrow y = \dfrac{{ - 4}}{3}\left( 0 \right) + 4\],
Now simplifying we get,
\[ \Rightarrow y = 4\],
So, the \[y\]-intercept will be \[\left( {0,4} \right)\],
Now assume \[y = 0\] to find the \[x\]-intercept, substituting the value of \[y\] in the equation we get,
\[ \Rightarrow 0 = \dfrac{{ - 4}}{3}x + 4\],
Now subtracting 4 on both sides we get,
\[ \Rightarrow 0 - 4 = \dfrac{{ - 4}}{3}x + 4 - 4\],
Now eliminating the like terms we get,
\[ \Rightarrow - 4 = \dfrac{{ - 4}}{3}x\],
Now simplifying we get,
\[ \Rightarrow \dfrac{1}{3}x = 1\],
Now multiplying 3 on both sides, we get,
\[ \Rightarrow \dfrac{1}{3}x \times 3 = 1 \times 3\],
Now further simplification we get,
\[ \Rightarrow x = 3\],
So, \[x\]-intercept will be \[\left( {3,0} \right)\].
Plotting the points on the graph we get,

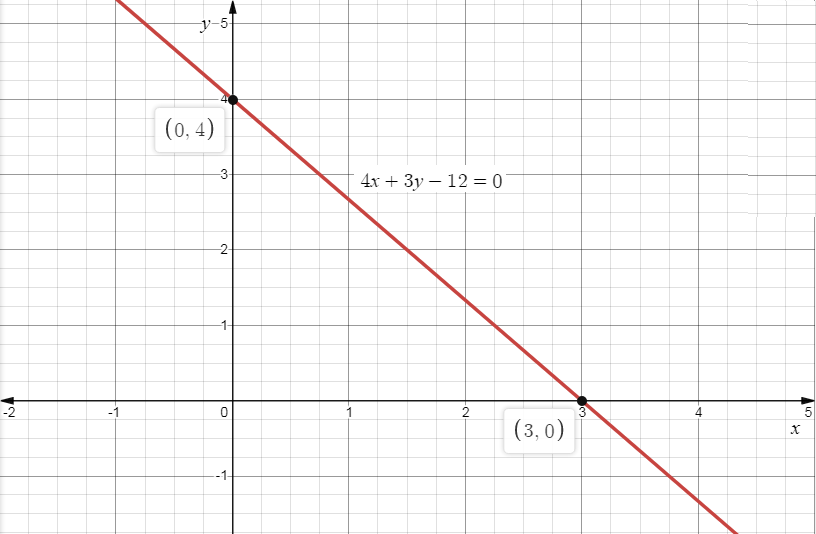
Note: A linear graph is a single straight line, to draw a linear graph, we need to locate some points on the graph, join these points if the line joining these points is a straight line, then the graph is a linear graph.
We can plot the linear graph by 3 methods, they are:
Plotting points: Assuming the values for \[x\] and find the corresponding value of \[y\], plot the points on the graph.
X- and Y- intercepts: If we have to find \[x\]-intercept we have to put \[y = 0\], and if we have to find \[y\]-intercept we have to put \[x = 0\], now plot the points on the graph.
Slope-intercept form: Plot the point after finding the \[y\]-intercept, now use the slope and find another point and plot the point using \[y\]-intercept, by joining the points we will get the straight line.