
How do you graph $3x + y = - 2$?
Answer
547.2k+ views
Hint: First, we have to make the given linear equation in Slope-intercept form and then calculate the value of $y$ for any two arbitrary values of $x$. Next make a table of these values of $x$ and $y$. Next plot the obtained points on the graph paper and draw a line passing through these points.
Formula used:
Slope Intercept of a line:
The equation of a line with slope $m$ and making an intercept $c$ on $y$-axis is $y = mx + c$.
Complete step by step answer:
Given linear equation in two variables: $3x + y = - 2$
First, we have to make the given linear equation in Slope-intercept form.
So, subtract $3x$ from both sides of the equation.
$y = - 2 - 3x$
Now, we have to calculate the value of $y$ for any two arbitrary values of $x$. Thus, finding the value of $y$ when $x = 0$ and $x = 1$.
When $x = 0$, $y = - 2 - 3 \cdot 0 = - 2$
When $x = 1$, $y = - 2 - 3 \cdot 1 = - 5$
Now we have to make a table of these values of $x$ and $y$.
Now we have to plot the points $A\left( {0, - 2} \right)$ and $B\left( {1, - 5} \right)$ on the graph paper and draw a line passing through $A$ and $B$.
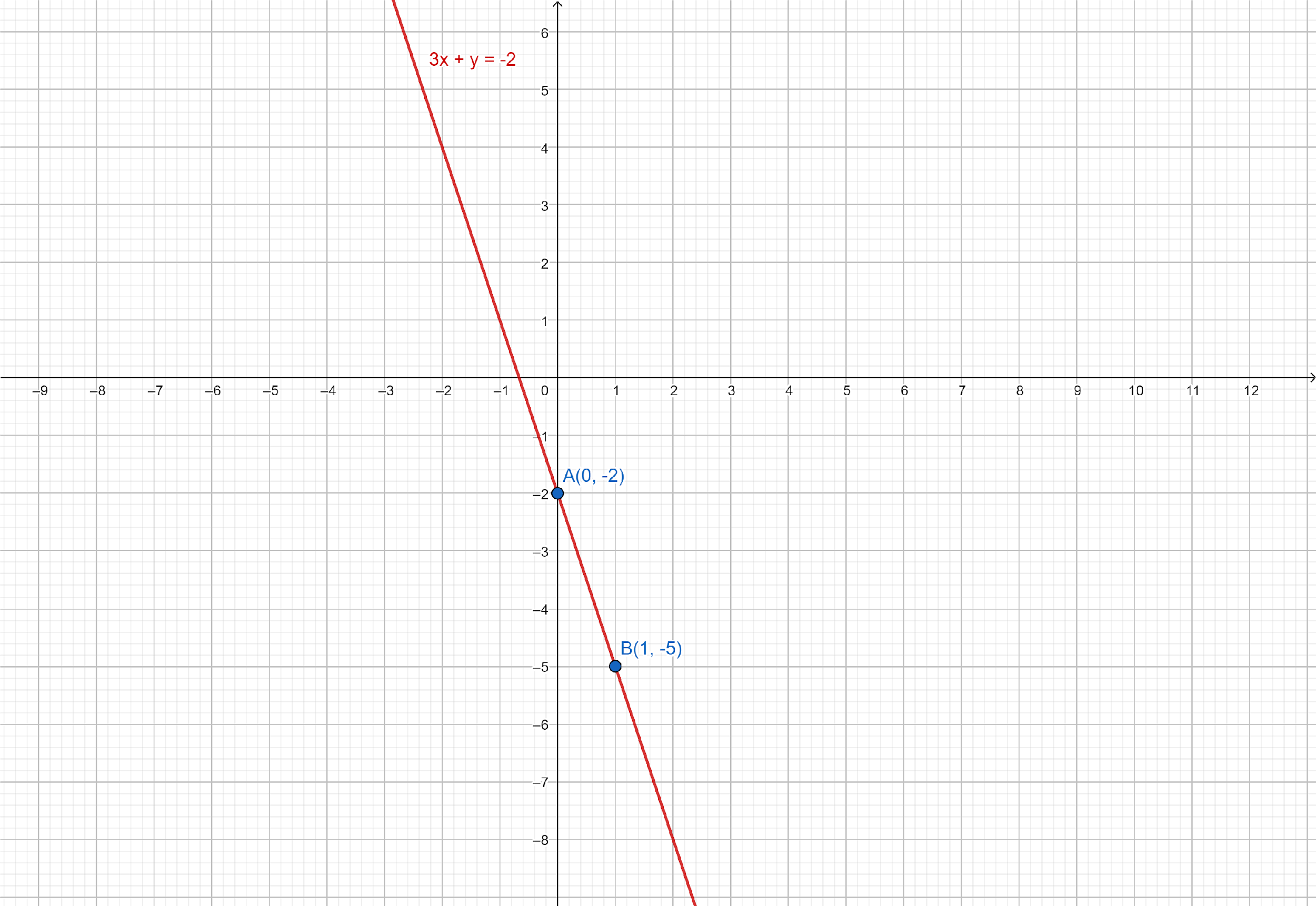
Final solution: Hence, the straight line, so obtained, is the required graph of the given linear equation.
Note: Method to draw the graph of linear equation in two variables:
Step I: Write a given linear equation and express y in terms of x.
Step II: Put different values of x and find the corresponding value of y.
Step III: Form a table by writing the values of y below the corresponding values of x.
Step IV: Plot these points on graph paper.
Step V: Join these points. Thus, we get a straight line and produce it on both sides.
Hence, the straight line, so obtained, is the required graph of the given linear equation.
Formula used:
Slope Intercept of a line:
The equation of a line with slope $m$ and making an intercept $c$ on $y$-axis is $y = mx + c$.
Complete step by step answer:
Given linear equation in two variables: $3x + y = - 2$
First, we have to make the given linear equation in Slope-intercept form.
So, subtract $3x$ from both sides of the equation.
$y = - 2 - 3x$
Now, we have to calculate the value of $y$ for any two arbitrary values of $x$. Thus, finding the value of $y$ when $x = 0$ and $x = 1$.
When $x = 0$, $y = - 2 - 3 \cdot 0 = - 2$
When $x = 1$, $y = - 2 - 3 \cdot 1 = - 5$
Now we have to make a table of these values of $x$ and $y$.
| $x$ | $0$ | $1$ |
| $y$ | $ - 2$ | $ - 5$ |
Now we have to plot the points $A\left( {0, - 2} \right)$ and $B\left( {1, - 5} \right)$ on the graph paper and draw a line passing through $A$ and $B$.

Final solution: Hence, the straight line, so obtained, is the required graph of the given linear equation.
Note: Method to draw the graph of linear equation in two variables:
Step I: Write a given linear equation and express y in terms of x.
Step II: Put different values of x and find the corresponding value of y.
Step III: Form a table by writing the values of y below the corresponding values of x.
Step IV: Plot these points on graph paper.
Step V: Join these points. Thus, we get a straight line and produce it on both sides.
Hence, the straight line, so obtained, is the required graph of the given linear equation.
Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE

10 examples of friction in our daily life




