
How do you graph $ 2x - 1 = y $ ?
Answer
549.3k+ views
Hint: In order to graph the above equation, consider the fact the graph to any linear function of the form $ ax + by + c = 0 $ is always a straight line ..As to plot a straight line we require two points. One point is the x-intercept obtained by putting $ y = 0 $ and another is the y-intercept obtained by putting $ x = 0 $ in the equation. By plotting, these two points and connect them to obtain the straight line of the equation.
Complete step-by-step answer:
We are given a linear equation in two variables $ x\,and\,y $ i.e. $ 2x - 1 = y $
As we know the graph to a linear function of the form $ ax + by + c = 0 $ is always a straight line.
So, in order to draw a line, we must have at least two points on the graph which we can connect to form a line.
We’ll be taking one point as y-intercept and another as x-intercept.
To calculate y-intercept of the graph, put $ x = 0 $ in the equation
$
2\left( 0 \right) - 1 = y \\
y = - 1 \;
$
We get y-intercept at point $ \left( {0, - 1} \right) $
Now To calculate x-intercept of the graph, put $ y = 0 $ in the equation
$
2x - 1 = y \\
2x - 1 = 0 \\
2x = 1 \\
x = \dfrac{1}{2} \\
x = 0.5 \;
$
We get x-intercept at point $ \left( {0.5,0} \right) $
Now the graph the equation, we are jumping on the cartesian plan and plot $ \left( {0, - 1} \right) $ , $ \left( {0.5,0} \right) $ .Joining these two points we get a straight line representing our equation $ 2x - 1 = y $
Graph of equation having y-intercept as $ \left( {0, - 1} \right) $ and x-intercept as $ \left( {0.5,0} \right) $ .
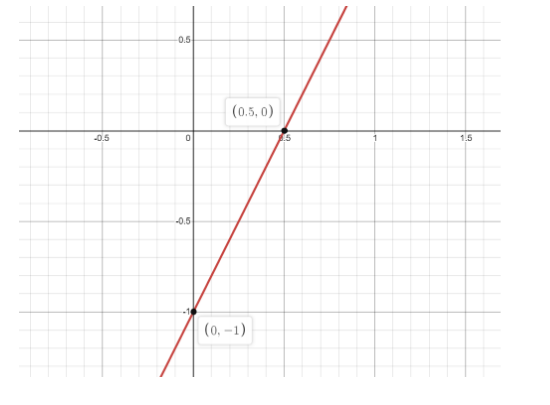
Note: 1.Draw the cartesian plane only with the help of straight ruler and pencil to get the perfect and accurate results.
2.Mark the points carefully.
3. x-intercept is the point at which the line intersects the x-axis of the plane and similarly y-intercept is the point at which line intersects the y-axis of the plane.
4.Slope-Intercept Form= $ y = mx + c $
Complete step-by-step answer:
We are given a linear equation in two variables $ x\,and\,y $ i.e. $ 2x - 1 = y $
As we know the graph to a linear function of the form $ ax + by + c = 0 $ is always a straight line.
So, in order to draw a line, we must have at least two points on the graph which we can connect to form a line.
We’ll be taking one point as y-intercept and another as x-intercept.
To calculate y-intercept of the graph, put $ x = 0 $ in the equation
$
2\left( 0 \right) - 1 = y \\
y = - 1 \;
$
We get y-intercept at point $ \left( {0, - 1} \right) $
Now To calculate x-intercept of the graph, put $ y = 0 $ in the equation
$
2x - 1 = y \\
2x - 1 = 0 \\
2x = 1 \\
x = \dfrac{1}{2} \\
x = 0.5 \;
$
We get x-intercept at point $ \left( {0.5,0} \right) $
| X | 0 | 0.5 |
| y | -1 | 0 |
Now the graph the equation, we are jumping on the cartesian plan and plot $ \left( {0, - 1} \right) $ , $ \left( {0.5,0} \right) $ .Joining these two points we get a straight line representing our equation $ 2x - 1 = y $
Graph of equation having y-intercept as $ \left( {0, - 1} \right) $ and x-intercept as $ \left( {0.5,0} \right) $ .

Note: 1.Draw the cartesian plane only with the help of straight ruler and pencil to get the perfect and accurate results.
2.Mark the points carefully.
3. x-intercept is the point at which the line intersects the x-axis of the plane and similarly y-intercept is the point at which line intersects the y-axis of the plane.
4.Slope-Intercept Form= $ y = mx + c $
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




