Question

How do you graph $2x + 8 = 0$?

Answer 1

Hint: In this question we have to graph the function which is a linear equation in one variable, to do this first we will solve the equation to get the value of the $x$, then by using the fact that when $x$ equals a number, $y$ can take on any value and it would not change the equality. This will form a vertical line.

Complete step by step solution:
Given function is $2x + 8 = 0$,
We have to graph the function, to do this first we will solve the equation,
Subtract 8 from both sides of the equation, we get,
$ \Rightarrow 2x + 8 - 8 = 0 - 8$,
Now simplifying we get,
$ \Rightarrow 2x = - 8$,
Now divide 2 both sides of the equation we get,
$\Rightarrow \dfrac{2x}{2}=\dfrac{-8}{2}$,
Now simplifying we get,
$ \Rightarrow x = - 4$,
When $x$ equals a number, $y$ can take on any value and it would not change the equality. We could think of the equation as having a $y$ value with 0 as a coefficient, so no matter what value $y$ takes, it will always multiply by 0. This will form a vertical line.
So, the graph will be as,

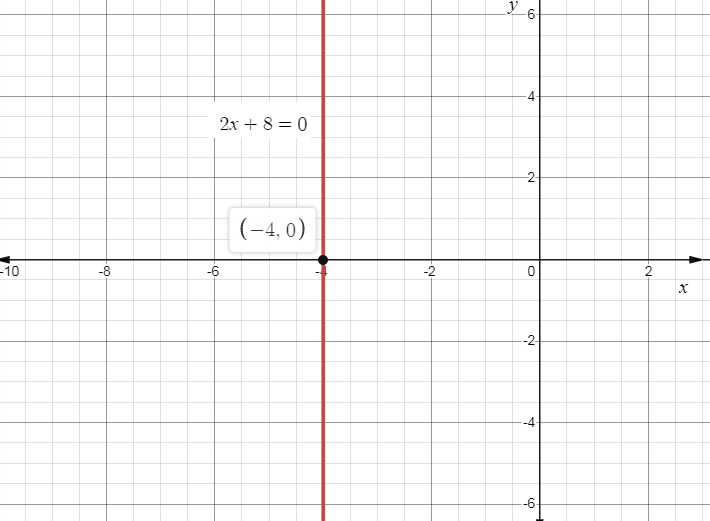
Note: On the coordinate plane, we know that each point must have a $x$ and a $y$ value. When we solved equations in one variable, it was easy to see that we had a $x$ value. What we didn't realize is that we also had a $y$ value as well. In fact, we had infinitely many $y$ values. Similarly, if we were to solve a one variable equation in terms of $y$, we would have infinitely many $x$ values. These equations do not form a point, but rather a horizontal or vertical line, and when $y$, equals a number then the graph will be a horizontal line, and When $x$ equals a number then the graph forms a vertical line.