Question

How do you find $\theta$ ?

Answer 1

Hint: The value of $\theta $ can be found by using sine and cosine functions. We start to solve the problem by finding the trigonometric functions $\sin \theta $ and $\cos \theta $ for the triangle. To get the value of $\theta $ , we multiply the trigonometric functions with their inverse functions.

Complete step-by-step solution:
The value of $\theta $ can be found out in 2 ways. We can easily find the value of $\theta $ with the use of two trigonometric functions $\sin \theta $ and $\cos \theta $
Case 1:
Firstly, The value of $\theta $ with help of sine function.
Sine is the trigonometric function of any specified angle that is used in the context of a right angle.
It is usually defined as the ratio of the length of the side opposite to an angle to the length of the hypotenuse of the right-angle triangle.
$\sin \theta $= length of the side opposite to angle $\theta $ is divided by the length of the hypotenuse.
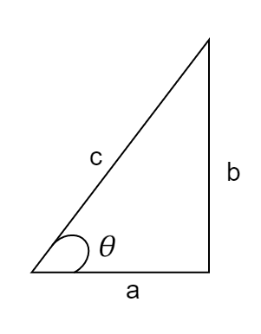
In the diagram given in the question,
The length of the side opposite to the angle $\theta $ is b.
The length of the hypotenuse is c.
Therefore, upon substituting we get,
$\Rightarrow \sin \theta =\dfrac{b}{c}$
Now, we must find the value of theta.
Multiplying the above equation with the inverse sine function, we get,
$\Rightarrow arcsin\left( \sin \theta \right)=arcsin\left( \dfrac{b}{c} \right)$
We know that $arcsin\left( \sin \theta \right)=\theta$
Substituting the same,
We get $\theta =\text{ }arcsin\left( \dfrac{b}{c} \right)$
Hence, the value of $\theta$ in terms of arcsine function is given by $\theta =\text{ }arcsin\left( \dfrac{b}{c} \right)$
Case 2:
Secondly, The value of $\theta$ with the help of cosine function.
Cos is the trigonometric function of any specified angle that is used in the context of a right angle.
It is usually defined as the ratio of the length of the side adjacent to an angle to the length of the hypotenuse of the right-angle triangle.
$\cos \theta$ = length of the side adjacent to angle $\theta$ is divided by the length of the hypotenuse.
In the diagram given in the question,
The length of the side adjacent to the angle $\theta$ is a.
The length of the hypotenuse is c.
$\cos \theta =\dfrac{a}{c}$
Now, we must find the value of theta.
Multiplying the above equation with the inverse cosine function, we get,
$\Rightarrow \arccos \left( \cos \theta \right)=\arccos \left( \dfrac{a}{c} \right)$
We know that $\arccos \left( \cos \theta \right)=\theta$
Substituting the same,
We get $\theta =\text{ }\arccos \left( \dfrac{a}{c} \right)$
Hence, the value of $\theta$ in terms of arcsine function is given by $\theta =\text{ }\arccos \left( \dfrac{a}{c} \right)$

Note: The inverse functions in trigonometry are also known as arc functions or anti trigonometric functions. They are majorly known as arc functions because they are most used to find the length of the arc needed to get the given or specified value. We can convert a function into an inverse function and vice versa.