Question

How do you find the vertex of $y=2{{x}^{2}}-4x$?

Answer 1

Hint: The given equation is linear in y and quadratic in x. Therefore, it is the equation of a parabola. For determining the vertex of the parabola, we have to simplify the expression of y using the completing the square method. For this, first we need to take $2$ common on the right hand side of the given equation to get $y=2\left( {{x}^{2}}-2x \right)$. Then we need to add and subtract the square of half of the coefficient of x, that is, ${{1}^{2}}$ inside the bracket to get $y=2\left( {{x}^{2}}-2x+{{1}^{2}}-{{1}^{2}} \right)$. Finally, using the identity ${{a}^{2}}-2ab+{{b}^{2}}={{\left( a-b \right)}^{2}}$ we can contract the RHS and on further simplifying, we will obtain the given equation as the standard equation of a parabola as $\left( y-k \right)=a{{\left( x-h \right)}^{2}}$ whose vertex lies at $\left( h,k \right)$.

Complete step by step solution:
The equation given in the above question is
$\Rightarrow y=2{{x}^{2}}-4x$
Since the above equation is linear in y and quadratic in x, we can say that it is the equation of a parabola. Now, for determining the vertex, let us try to convert it in the standard form of a parabola as $\left( y-k \right)=a{{\left( x-h \right)}^{2}}$. For this, we take $2$ common on the right hand side of the above equation to get
$\Rightarrow y=2\left( {{x}^{2}}-2x \right)$
Now, using the completing the square method, we add and subtract half of the coefficient of x inside the bracket, that is, ${{1}^{2}}$ to get
$\Rightarrow y=2\left( {{x}^{2}}-2x+{{1}^{2}}-{{1}^{2}} \right)$
Now, we know that ${{a}^{2}}-2ab+{{b}^{2}}={{\left( a-b \right)}^{2}}$. Using this identity we can write the above equation as
\[\begin{align}
  & \Rightarrow y=2\left( {{\left( x-1 \right)}^{2}}-{{1}^{2}} \right) \\
 & \Rightarrow y=2\left( {{\left( x-1 \right)}^{2}}-1 \right) \\
 & \Rightarrow y=2{{\left( x-1 \right)}^{2}}-2 \\
\end{align}\]
Adding \[2\] both sides, we get
$\begin{align}
  & \Rightarrow y+2=2{{\left( x-1 \right)}^{2}}-2+2 \\
 & \Rightarrow \left( y+2 \right)=2{{\left( x-1 \right)}^{2}} \\
\end{align}$
Comparing the above equation with the standard equation $\left( y-k \right)=a{{\left( x-h \right)}^{2}}$, we get
$\begin{align}
  & \Rightarrow h=1 \\
 & \Rightarrow k=-2 \\
\end{align}$
Hence, the coordinates of the vertex are obtained as $\left( 1,-2 \right)$.
We can graphically interpret this in the below figure.

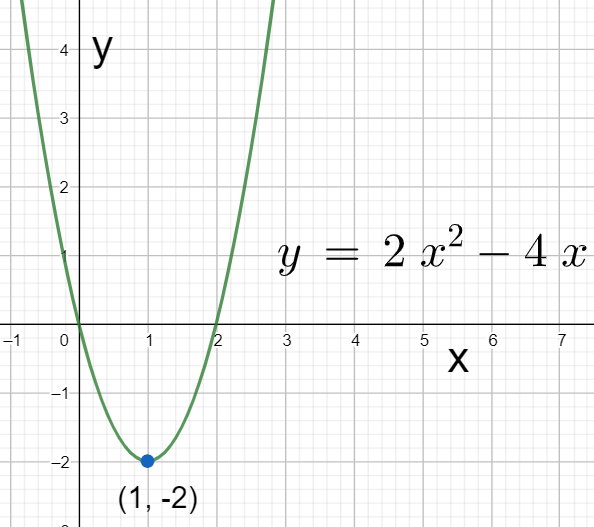
Note: We can also differentiate the given equation to get the slope or the derivative of the parabola and equate to zero so as to get the abscissa of the vertex. Then on substituting the abscissa into the given equation we can obtain the ordinate, and hence the coordinates of the vertex.