Question

How do you find the value of \[\csc ( - 210)?\]

Answer 1

Hint: We know that $\cos ec( - x) = - \cos ecx$ .
Again the function $y = \cos ecx$ has a period of $2\pi $ or ${360^ \circ }$ , i.e., the value of $\cos ecx$ repeats after an interval of $2\pi $ or ${360^ \circ }$ . Therefore we calculate the given period using the intervals. After that we use the trigonometric formulas and we get the required value.


Complete step by step answer:
We know that the function $y = \cos ecx$ has a period of $2\pi $ or ${360^ \circ }$ , i.e., the value of $\cos ecx$ repeats after an interval of $2\pi $ or ${360^ \circ }$ .
First we draw the graph of $y = \cos ecx$

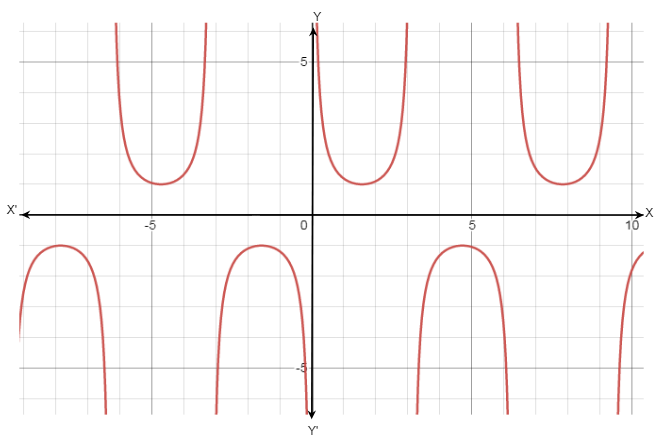
Now the given data ${120^ \circ } = {90^ \circ } + {30^ \circ }$
Therefore $\csc ( - 120)$
Using the property $\csc ( - x) = - \csc x$ , we get
$ - \csc (120)$
We can write the above statement as,
$ = - \csc (90 + 30)$
We know that $\csc x = \dfrac{1}{{\sin x}}$ , use this property and we get
$ = - \dfrac{1}{{\sin (90 + 30)}}$
We know that the property of trigonometric that is $\sin (90 + x) = \cos x$
Use this in the above function and we get
$ = - \dfrac{1}{{\cos 30}}$
From the value table we know the value of $\cos 30 = \dfrac{{\sqrt 3 }}{2} = \sin 60$ , put this in above equation and we get
$ = - \dfrac{1}{{\tfrac{{\sqrt 3 }}{2}}}$
Simplifying and we get
$ = - \dfrac{2}{{\sqrt 3 }}$
Therefore our required answer is $\csc ( - 120) = - \dfrac{2}{{\sqrt 3 }}$ .

Note:Note that formulas which is very important and try to remember all the times
$1.\sin x = \dfrac{1}{{\csc x}},\cos x = \dfrac{1}{{\sec x}},\tan x = \dfrac{1}{{\cot x}}$
$2.{\sin ^2}x + {\cos ^2}x = 1$
$3.{\sec ^2}x - {\tan ^2}x = 1$
$4.{\csc ^2}x - {\cot ^2}x = 1$
$5.\sin ( - x) = - \sin x$
$6.\cos ( - x) = \cos x$
$7.\tan ( - x) = - \tan x$
$8.\sin (2n\pi \pm x) = \sin x$ , period $2\pi $
$9.\cos (2n\pi \pm x) = \cos x$ , period $2\pi $
$10.\tan (n\pi \pm x) = \tan x$ , period $\pi $
WE also have to know about the sign conversion ,
In the first quadrant we know all the trigonometric functions are positive. In the second quadrant sine function is positive and others are negative. The third quadrant tangent is positive and in the fourth quadrant cos is positive. At least we must know about the trigonometric function value table. We have all the basic values of all trigonometric functions.