Question

How do you find the slope of $y=-5x$ ?

Answer 1

Hint: Slope of any curve at any particular point is $\tan \theta $ where $\theta $ is the angle made by the tangent at the particular point with positive x axis. Slope of a straight line is constant. It is the same at all points. $y=-5x$ is an equation of straight line. Slope of a straight line having equation $y=mx+c$ is m and c is the y intercept of the straight line.

Complete step by step answer:
We have to find the slope of $y=-5x$ which is a straight line.

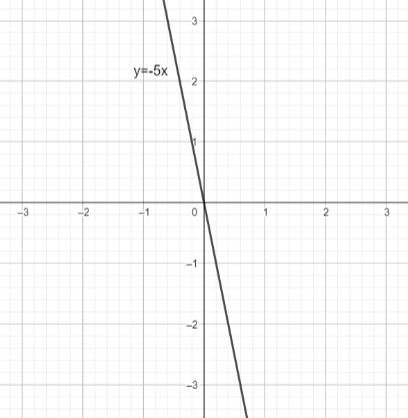
We know that the slope of a straight is constant. So slope of line having equation $y=mx+c$ is m
So if we compare $y=-5x$ with equation $y=mx+c$ then m=-5 and c=0 so the slope of $y=-5x$ is -5.
If the straight is in the form $ax+by+c=0$ then we have to convert the equation in the form of $y=mx+c$.
$ax+by+{{c}_{1}}=0$
$\Rightarrow y=\dfrac{-a}{b}x+\dfrac{-{{c}_{1}}}{b}$
Now we can compare $y=\dfrac{-a}{b}x+\dfrac{-{{c}_{1}}}{b}$ with $y=mx+c$ our slope will be $\dfrac{-a}{b}$ and the y intercept is $\dfrac{-{{c}_{1}}}{b}$.
Another method is by differentiation. The slope of function $y=f\left( x \right)$ at any particular point ${{x}_{0}}$is $f'\left( {{x}_{0}} \right)$ where $f'\left( {{x}_{0}} \right)$ is the derivative of $f\left( x \right)$ with respect to x at point ${{x}_{0}}$.
 We have a function $y=-5x$ so we can differentiate $-5x$ with respect to x . In this case the point will not be required as result of differentiation will be constant because the slope of a straight line is constant .

Applying differentiation the slope of $y=-5x$ is $\dfrac{d(-5x)}{dx}$ which is equal to -5.

Note: Remember we can find the slope at any point of any function by differentiating the function with respect to x when y is a pure function of x it should not contain any other variable
For example in $y={{x}^{2}}+{{z}^{2}}$ we can’t just differentiate with respect to x because z is also a variable so now it is a 3 dimensional problem it can have multiple slopes at one point. It becomes a problem of 3 dimensional geometry.