Question

How do you find the slope of a line?

Answer 1

Hint: Find the ratio of change in x and change in y.
We can find the slope in two ways by plotting in the graph and observing $ \dfrac{{\vartriangle x}}{{\vartriangle y}} $ which is the ratio of change of x and change of y or else we can use a direct formula where we can directly substitute in the formula of slope of line with two distinct points and find the slope.

Complete step-by-step answer:
Method 1:
First, we are going to get the slope of a graph

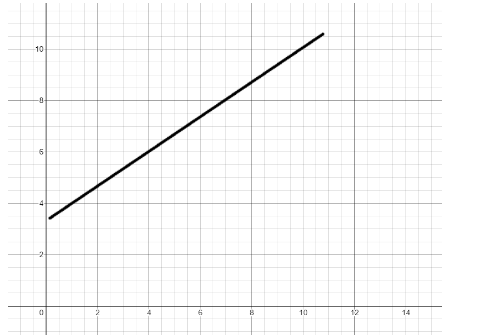
Consider the graph, we are going to find the slope of this line, by considering any two points on the line. And then we find the change in x which is \[\vartriangle x\] and change in y which is $ \vartriangle y $ .
We will draw a line parallel to the x-axis until we reach a point such, we get the change in x and similarly we will get the change in y as well, as shown in the figure below.

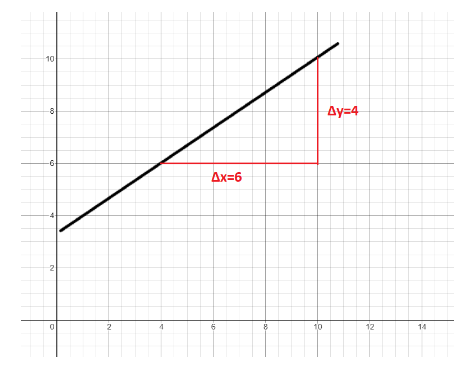
Then we find the ratio of these which will give us the slope.
 $ Slope = \dfrac{{\vartriangle x}}{{\vartriangle y}} $
 $ slope = \dfrac{6}{4} = \dfrac{3}{2} $

Method 2:
We are directly going to use the formula for slope of a line when two distinct points are given which is
 $ slope = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}} $
Where $ \left( {{x_1},{y_1}} \right) $ and $ \left( {{x_2},{y_2}} \right) $ are the two distinct points which lie on the line whose slope we have to calculate.
For the points $ (3,1) $ and $ (4,1) $ . The slope is
 $ Slope = \dfrac{{1 - 1}}{{4 - 3}} = 0 $

Note: In the formula of slope, there is no specific order for consider any point for $ \left( {{x_1},{y_1}} \right) $ or $ \left( {{x_2},{y_2}} \right) $ , as the resultant slope that we get on considering either of those scenarios, we are going to get the same resultant slope for the given two points.