Question

How do you find scale factor?

Answer 1

Hint: Here we must know what scale factor is. It is actually the comparison between two similar things which tells us about the scale or the ratio of length of the larger to the smaller to the larger between two similar figures. The scale factor from larger to smaller will be greater than one and from smaller to larger will be less than one.

Complete step-by-step answer:
Here we are given to define the scale factor. Scale factor is calculated between two similar things. The example can make it clearer.
Let us take two similar rectangles, say $ABCD{\text{ and }}EFGH$ and their sides are in the ratio. Here $ABCD$ is the smaller rectangle while $EFGH$ is the larger rectangle. So let us draw their figures as:

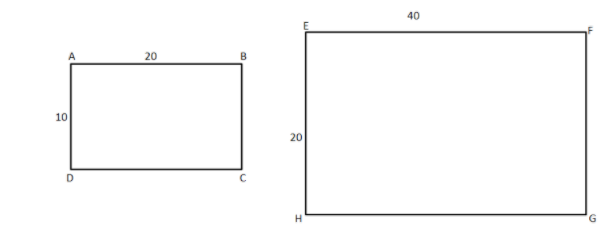
Here we can see that both the rectangles are similar but only vary in their sizes. The bigger rectangle is twice the length and breadth as compared to the smaller one. So her if we want to find the scale factor from smaller to the larger rectangle, we can use the formula:
${\text{scale factor}} = \dfrac{{{\text{dimension of new shape}}}}{{{\text{dimension of original shape}}}}$
As here we are finding the scale factor from the smaller to the larger. So we will say that the smaller dimension will be the dimension of the original shape and as we are going to the larger one so it will be the dimension of the new shape. So we can say that:
${\text{scale factor}} = \dfrac{{{\text{dimension of new shape}}}}{{{\text{dimension of original shape}}}} = \dfrac{{40}}{{20}} = 2$
Similarly if we find the scale factor from larger to the smaller shape, then the dimension of the larger will be the dimension of the original shape. Now we will get:
${\text{scale factor}} = \dfrac{{{\text{dimension of new shape}}}}{{{\text{dimension of original shape}}}} = \dfrac{{20}}{{40}} = 0.5$
So we can say that scale factor tells us how much bigger or smaller the new similar figure is from the original one.

Note: Here the student must remember than when we are given two similar figures and we need to find the scale factor we must apply the formula
${\text{scale factor}} = \dfrac{{{\text{dimension of new shape}}}}{{{\text{dimension of original shape}}}}$
Also we can be given the scale factor and the new or original dimension, so then also we need to apply the same formula and get the required value.